Sign in
Please select an account to continue using cracku.in
↓ →
Shruti travels a distance of 224 km in four parts for a total travel time of 3 hours. Her speeds in these four parts follow an arithmetic progression, and the corresponding time taken to cover these four parts follow another arithmetic progression. If she travels at a speed of 960 meters per minute for 30 minutes to cover the first part, then the distance, in meters, she travels in the fourth part is
According to question, Shruti travels a distance of 224 km in four parts for a total travel time of 3 hours.
Given, in the first part time required is 30 minutes.
Also, the time taken to cover these four parts follow arithmetic progression.
So, let us say the times be 30 minutes, (30+d) minutes, (30+2d) minutes and (30+3d) minutes
So, $$30+\left(30+d\right)+\left(30+2d\right)+\left(30+3d\right)=180$$
or, $$6d=180-120$$
or, $$6d=60$$
or, $$d=\dfrac{60}{6}=10$$ minutes.
So, the time required in these four parts are 30 minutes, 40 minutes, 50 minutes and 60 minutes respectively.
Now, in the first part, speed is 960 metres per minute.
Speed in the four parts is also in arithmetic progression.
Let's say the speeds be $$(960+x)$$,$$(960+2x)$$,$$(960+3x)$$ metres per minute
So, total distance covered = $$960\times\ 30+\left(960+x\right)\times\ 40+\left(960+2x\right)\times\ 50+\left(960+3x\right)\times\ 60$$ metres
So, $$960\times\ 30+\left(960+x\right)\times\ 40+\left(960+2x\right)\times\ 50+\left(960+3x\right)\times\ 60=224000$$
or, $$960\left(30+40+50+60\right)+40x+\left(2x\right)\left(50\right)+\left(3x\right)\left(60\right)=224000$$
or, $$172800+320x=224000$$
or, $$320x=224000-172800=51200$$
or, $$x=\dfrac{51200}{320}=160$$
So, the speed in the fourth part is $$960+3x=960+3\times\ 160=1440$$ metres per minute
Time in the fourth part is 60 minutes
So, distance covered in the fourth part = $$1440\times\ 60=86400$$ metres
So, option D is the correct answer.
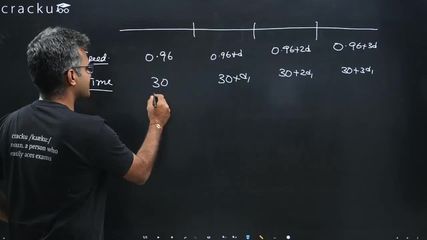
Click on the Email ☝️ to Watch the Video Solution
Create a FREE account and get:
Educational materials for CAT preparation