Sign in
Please select an account to continue using cracku.in
↓ →
A value of $$c$$ for which the minimum value of $$f(x)=x^{2}-4cx+8c$$ is greater than the maximum value of $$g(x)=-x^{2}+3cx-2c$$, is
First function $$f\left(x\right)=x^2-4cx+8$$
For this function $$a>0$$, so minimum value will occur at $$x=-\dfrac{b}{2a}=-\left(-\dfrac{4c}{2}\right)=2c$$
So, the minimum value of the function is = $$2c^2-4c\left(2c\right)+8c=-4c^2+8c$$
Second function $$g(x)=-x^{2}+3cx-2c$$
For this function $$a<0$$, so maximum value will occur at $$x=-\dfrac{b}{2a}=-\dfrac{\left(-3c\right)}{2}=\dfrac{3c}{2}$$
So, the maximum value of the function is = $$-\left(\dfrac{3c}{2}\right)^2+3c\left(\dfrac{3c}{2}\right)-2c=\dfrac{9c^2}{4}-2c$$
So, as per the given condition,
$$\dfrac{9c^2}{4}-2c<-4c^2+8c$$
or, $$\dfrac{9c^2}{4}+4c^2<8c+2c$$
or, $$\dfrac{25c^2}{4}<10c$$
or, $$\dfrac{5c^2}{4}<2c$$
or, $$5c^2<8c$$
or, $$5c^2-8c<0$$
or, $$c\left(c-\dfrac{8}{5}\right)<0$$
or, $$0<c<\dfrac{8}{5}$$
So, the value of $$c$$ which lies in this range is $$\dfrac{1}{2}$$
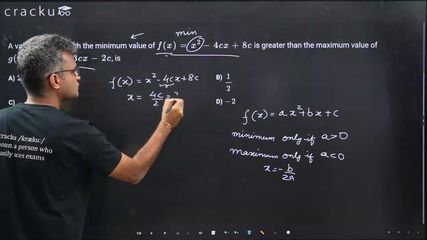
Click on the Email ☝️ to Watch the Video Solution
Create a FREE account and get:
Educational materials for CAT preparation