CAT 2019 Slot 2 Question Paper
For the following questions answer them individually
CAT 2019 Slot 2 - Question 71
Two ants A and B start from a point P on a circle at the same time, with A moving clock-wise and B moving anti-clockwise. They meet for the first time at 10:00 am when A has covered 60% of the track. If A returns to P at 10:12 am, then B returns to P at
CAT 2019 Slot 2 - Question 72
Let $$a_1, a_2, ...$$ be integers such that
$$a_1 - a_2 + a_3 - a_4 + .... + (-1)^{n - 1} a_n = n,$$ for all $$n \geq 1.$$
Then $$a_{51} + a_{52} + .... + a_{1023}$$ equals
CAT 2019 Slot 2 - Question 73
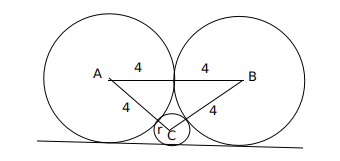
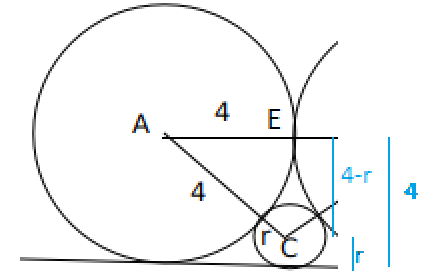
Two circles, each of radius 4 cm, touch externally. Each of these two circles is touched externally by a third circle. If these three circles have a common tangent, then the radius of the third circle, in cm, is
CAT 2019 Slot 2 - Question 74
Let A be a real number. Then the roots of the equation $$x^2 - 4x - log_{2}{A} = 0$$ are real and distinct if and only if
CAT 2019 Slot 2 - Question 75
The quadratic equation $$x^2 + bx + c = 0$$ has two roots 4a and 3a, where a is an integer. Which of the following is a possible value of $$b^2 + c$$?
CAT 2019 Slot 2 - Question 76
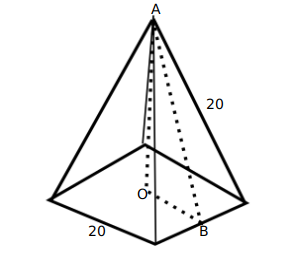
The base of a regular pyramid is a square and each of the other four sides is an equilateral triangle, length of each side being 20 cm. The vertical height of the pyramid, in cm, is
CAT 2019 Slot 2 - Question 77
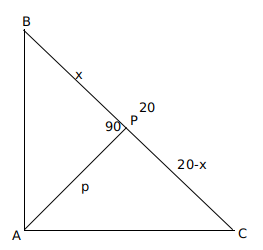
Let ABC be a right-angled triangle with hypotenuse BC of length 20 cm. If AP is perpendicular on BC, then the maximum possible length of AP, in cm, is
CAT 2019 Slot 2 - Question 78
If x is a real number, then $$\sqrt{\log_{e}{\frac{4x - x^2}{3}}}$$ is a real number if and only if
CAT 2019 Slot 2 - Question 79
If $$5^x - 3^y = 13438$$ and $$5^{x - 1} + 3^{y + 1} = 9686$$, then x + y equals
789
456
123
0.-
Clear All
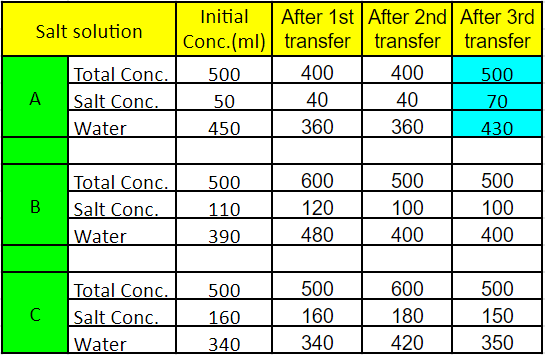
CAT 2019 Slot 2 - Question 80
The strength of a salt solution is p% if 100 ml of the solution contains p grams of salt. Each of three vessels A, B, C contains 500 ml of salt solution of strengths 10%, 22%, and 32%, respectively. Now, 100 ml of the solution in vessel A is transferred to vessel B. Then, 100 ml of the solution in vessel B is transferred to vessel C. Finally, 100 ml of the solution in vessel C is transferred to vessel A. The strength, in percentage, of the resulting solution in vessel A is
Two Factor Authentication
Incase of any issue contact support@cracku.in