CAT 2018 Slot 1 DILR Question Paper
Adriana, Bandita, Chitra, and Daisy are four female students, and Amit, Barun, Chetan, and Deb are four male students. Each of them studies in one of three institutes - X, Y, and Z. Each student majors in one subject among Marketing, Operations, and Finance, and minors in a different one among these three subjects. The following facts are known about the eight students:
1. Three students are from X, three are from Y, and the remaining two students, both female, are from Z.
2. Both the male students from Y minor in Finance, while the female student from Y majors in Operations.
3. Only one male student majors in Operations, while three female students minor in Marketing.
4. One female and two male students major in Finance.
5. Adriana and Deb are from the same institute. Daisy and Amit are from the same institute.
6. Barun is from Y and majors in Operations. Chetan is from X and majors in Finance.
7. Daisy minors in Operations.
CAT 2018 Slot 1 DILR - Question 38
If Chitra majors in Finance, which subject does Bandita major in?
An ATM dispenses exactly Rs. 5000 per withdrawal using 100, 200 and 500 rupee notes. The ATM requires every customer to give her preference for one of the three denominations of notes. It then dispenses notes such that the number of notes of the customer’s preferred denomination exceeds the total number of notes of other denominations dispensed to her.
CAT 2018 Slot 1 DILR - Question 39
In how many different ways can the ATM serve a customer who gives 500 rupee notes as her preference?
789
456
123
0.-
Clear All
CAT 2018 Slot 1 DILR - Question 40
If the ATM could serve only 10 customers with a stock of fifty 500 rupee notes and a sufficient number of notes of other denominations, what is the maximum number of customers among these 10 who could have given 500 rupee notes as their preferences?
789
456
123
0.-
Clear All
CAT 2018 Slot 1 DILR - Question 41
What is the maximum number of customers that the ATM can serve with a stock of fifty 500 rupee notes and a sufficient number of notes of other denominations, if all the customers are to be served with at most 20 notes per withdrawal?
CAT 2018 Slot 1 DILR - Question 42
What is the number of 500 rupee notes required to serve 50 customers with 500 rupee notes as their preferences and another 50 customers with 100 rupee notes as their preferences, if the total number of notes to be dispensed is the smallest possible?
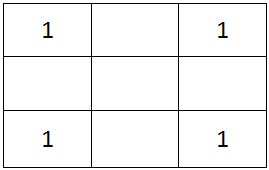
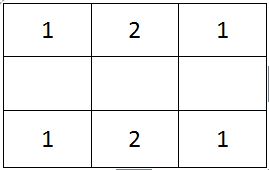
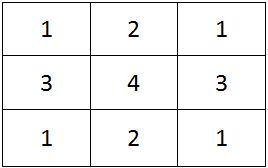
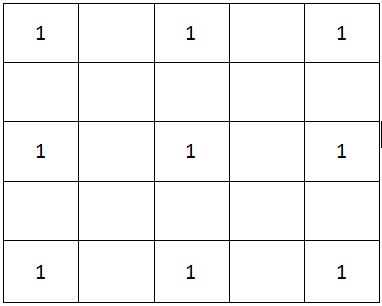
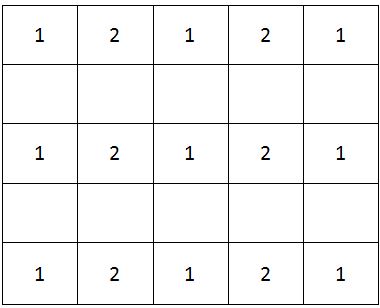
You are given an n×n square matrix to be filled with numerals so that no two adjacent cells have the same numeral. Two cells are called adjacent if they touch each other horizontally, vertically or diagonally. So a cell in one of the four corners has three cells adjacent to it, and a cell in the first or last row or column which is not in the corner has five cells adjacent to it. Any other cell has eight cells adjacent to it.
CAT 2018 Slot 1 DILR - Question 43
What is the minimum number of different numerals needed to fill a 3×3 square matrix?
789
456
123
0.-
Clear All
CAT 2018 Slot 1 DILR - Question 44
What is the minimum number of different numerals needed to fill a 5×5 square matrix?
789
456
123
0.-
Clear All
CAT 2018 Slot 1 DILR - Question 45
Suppose you are allowed to make one mistake, that is, one pair of adjacent cells can have the same numeral. What is the minimum number of different numerals required to fill a 5×5 matrix?
CAT 2018 Slot 1 DILR - Question 46
Suppose that all the cells adjacent to any particular cell must have different numerals. What is the minimum number of different numerals needed to fill a 5×5 square matrix?
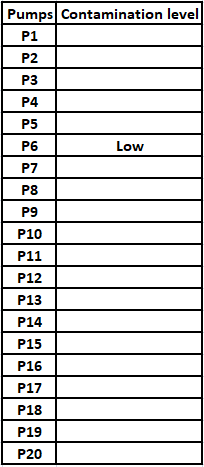
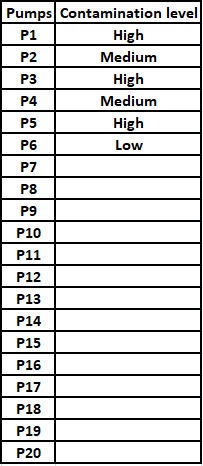
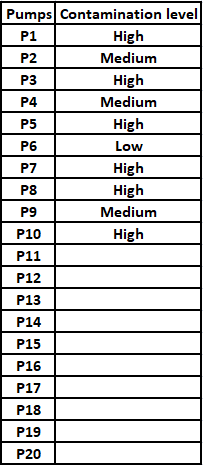
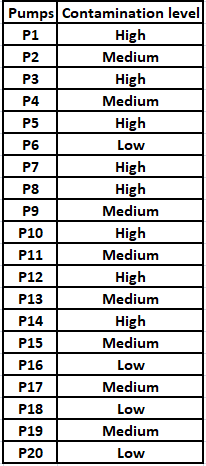
Fuel contamination levels at each of 20 petrol pumps P1, P2, …, P20 were recorded as either high, medium, or low.
1. Contamination levels at three pumps among P1 - P5 were recorded as high.
2. P6 was the only pump among P1 - P10 where the contamination level was recorded as low.
3. P7 and P8 were the only two consecutively numbered pumps where the same levels of contamination were recorded.
4. High contamination levels were not recorded at any of the pumps P16 - P20.
5. The number of pumps where high contamination levels were recorded was twice the number of pumps where low contamination levels were recorded.
CAT 2018 Slot 1 DILR - Question 48
What best can be said about the number of pumps at which the contamination levels were recorded as medium?
CAT 2018 Slot 1 DILR - Question 49
If the contamination level at P11 was recorded as low, then which of the following MUST be true?
CAT 2018 Slot 1 DILR - Question 50
If contamination level at P15 was recorded as medium, then which of the following MUST be FALSE?
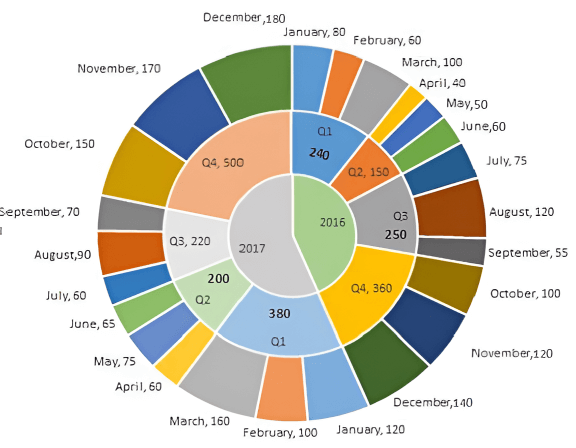
The multi-layered pie-chart below shows the sales of LED television sets for a big retail electronics outlet during 2016 and 2017. The outer layer shows the monthly sales during this period, with each label showing the month followed by sales figure of that month. For some months, the sales figures are not given in the chart. The middle-layer shows quarterwise aggregate sales figures (in some cases, aggregate quarter-wise sales numbers are not given next to the quarter). The innermost layer shows annual sales. It is known that the sales figures during the three months of the second quarter (April, May, June) of 2016 form an arithmetic progression, as do the three monthly sales figures in the fourth quarter (October, November, December) of that year.
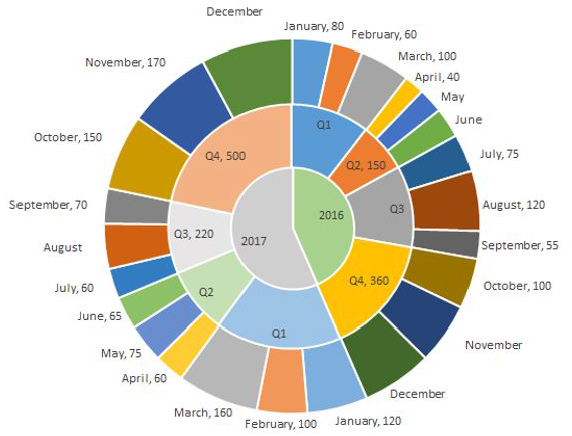
CAT 2018 Slot 1 DILR - Question 51
What is the percentage increase in sales in December 2017 as compared to the sales in December 2016?
CAT 2018 Slot 1 DILR - Question 52
In which quarter of 2017 was the percentage increase in sales from the same quarter of 2016 the highest?
CAT 2018 Slot 1 DILR - Question 53
During which quarter was the percentage decrease in sales from the previous quarter’s sales the highest?
CAT 2018 Slot 1 DILR - Question 54
During which month was the percentage increase in sales from the previous month’s sales the highest?
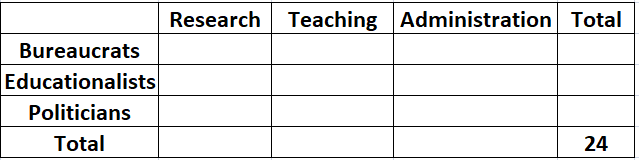
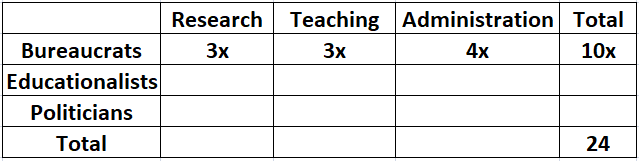
Twenty four people are part of three committees which are to look at research, teaching, and administration respectively. No two committees have any member in common. No two committees are of the same size. Each committee has three types of people: bureaucrats, educationalists, and politicians, with at least one from each of the three types in each committee. The following facts are also known about the committees:
1. The numbers of bureaucrats in the research and teaching committees are equal, while the number of bureaucrats in the research committee is 75% of the number of bureaucrats in the administration committee.
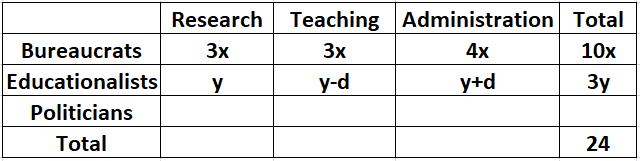
2. The number of educationalists in the teaching committee is less than the number of educationalists in the research committee. The number of educationalists in the research committee is the average of the numbers of educationalists in the other two committees.
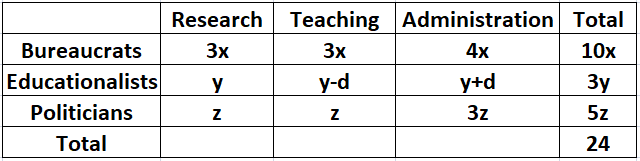
3. 60% of the politicians are in the administration committee, and 20% are in the teaching committee.
CAT 2018 Slot 1 DILR - Question 55
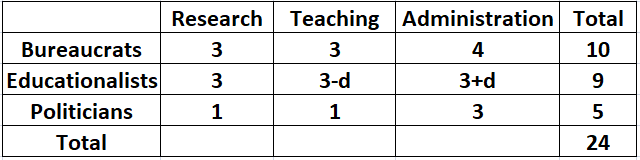
Based on the given information, which of the following statements MUST be FALSE?
CAT 2018 Slot 1 DILR - Question 56
What is the number of bureaucrats in the administration committee?
789
456
123
0.-
Clear All
CAT 2018 Slot 1 DILR - Question 57
What is the number of educationalists in the research committee?
789
456
123
0.-
Clear All
CAT 2018 Slot 1 DILR - Question 58
Which of the following CANNOT be determined uniquely based on the given information?
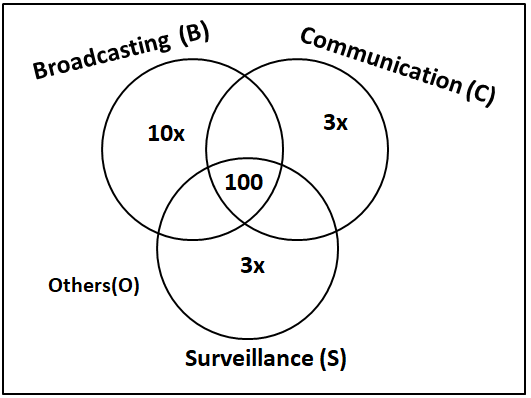
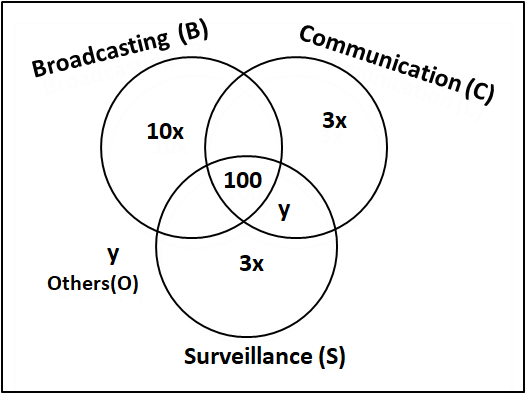
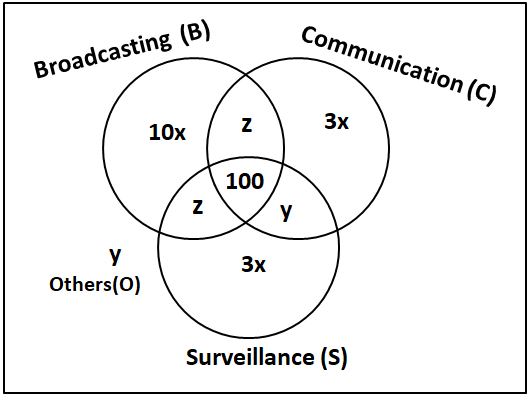
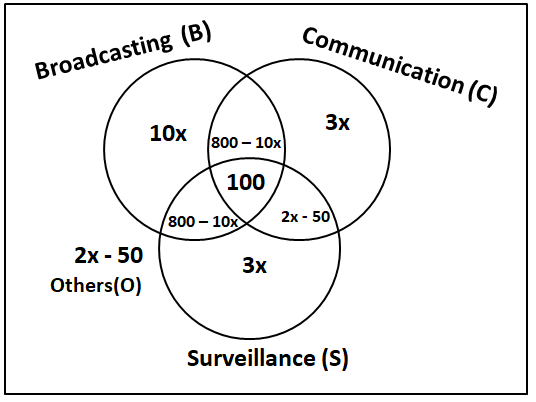
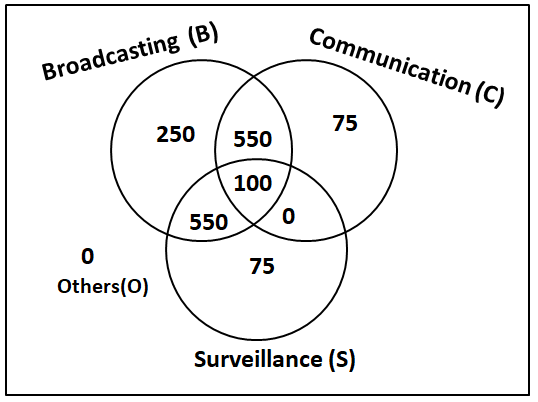
1600 satellites were sent up by a country for several purposes. The purposes are classified as broadcasting (B), communication (C), surveillance (S), and others (O). A satellite can serve multiple purposes; however a satellite serving either B, or C, or S does not serve O. The following facts are known about the satellites:
1. The numbers of satellites serving B, C, and S (though may be not exclusively) are in the ratio 2:1:1.
2. The number of satellites serving all three of B, C, and S is 100.
3. The number of satellites exclusively serving C is the same as the number of satellites exclusively serving S. This number is 30% of the number of satellites exclusively serving B.
4. The number of satellites serving O is the same as the number of satellites serving both C and S but not B.
CAT 2018 Slot 1 DILR - Question 59
What best can be said about the number of satellites serving C?
CAT 2018 Slot 1 DILR - Question 60
What is the minimum possible number of satellites serving B exclusively?
CAT 2018 Slot 1 DILR - Question 61
If at least 100 of the 1600 satellites were serving O, what can be said about the number of satellites serving S?
CAT 2018 Slot 1 DILR - Question 62
If the number of satellites serving at least two among B, C, and S is 1200, which of the following MUST be FALSE?
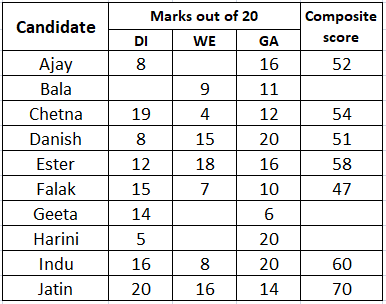
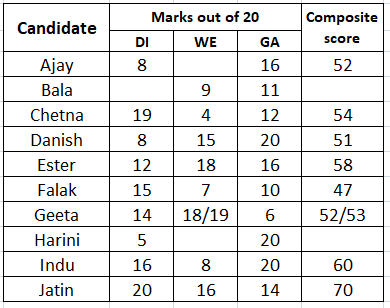
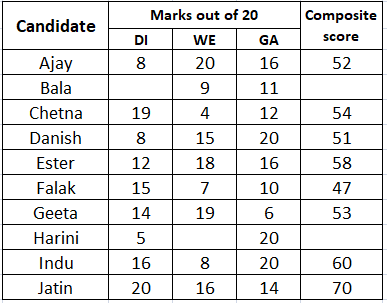
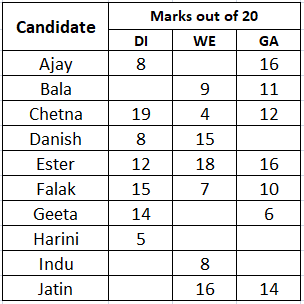
A company administers a written test comprising of three sections of 20 marks each - Data Interpretation (DI), Written English (WE) and General Awareness (GA), for recruitment. A composite score for a candidate (out of 80) is calculated by doubling her marks in DI and adding it to the sum of her marks in the other two sections. Candidates who score less than 70% marks in two or more sections are disqualified. From among the rest, the four with the highest composite scores are recruited. If four or less candidates qualify, all who qualify are recruited.
Ten candidates appeared for the written test. Their marks in the test are given in the table below. Some marks in the table are missing, but the following facts are known:
1. No two candidates had the same composite score.
2. Ajay was the unique highest scorer in WE.
3. Among the four recruited, Geeta had the lowest composite score.
4. Indu was recruited.
5. Danish, Harini, and Indu had scored the same marks the in GA.
6. Indu and Jatin both scored 100% in exactly one section and Jatin’s composite score was 10 more than Indu’s.
CAT 2018 Slot 1 DILR - Question 63
Which of the following statements MUST be true?
1. Jatin's composite score was more than that of Danish.
2. Indu scored less than Chetna in DI.
3. Jatin scored more than Indu in GA.
CAT 2018 Slot 1 DILR - Question 65
If all the candidates except Ajay and Danish had different marks in DI, and Bala's composite score was less than Chetna's composite score, then what is the maximum marks that Bala could have scored in DI?
789
456
123
0.-
Clear All
CAT 2018 Slot 1 DILR - Question 66
If all the candidates scored different marks in WE then what is the maximum marks that Harini could have scored in WE?
789
456
123
0.-
Clear All
Two Factor Authentication
Incase of any issue contact support@cracku.in