Please enter the following details
A company administers a written test comprising of three sections of 20 marks each - Data Interpretation (DI), Written English (WE) and General Awareness (GA), for recruitment. A composite score for a candidate (out of 80) is calculated by doubling her marks in DI and adding it to the sum of her marks in the other two sections. Candidates who score less than 70% marks in two or more sections are disqualified. From among the rest, the four with the highest composite scores are recruited. If four or less candidates qualify, all who qualify are recruited.
Ten candidates appeared for the written test. Their marks in the test are given in the table below. Some marks in the table are missing, but the following facts are known:
1. No two candidates had the same composite score.
2. Ajay was the unique highest scorer in WE.
3. Among the four recruited, Geeta had the lowest composite score.
4. Indu was recruited.
5. Danish, Harini, and Indu had scored the same marks the in GA.
6. Indu and Jatin both scored 100% in exactly one section and Jatin’s composite score was 10 more than Indu’s.
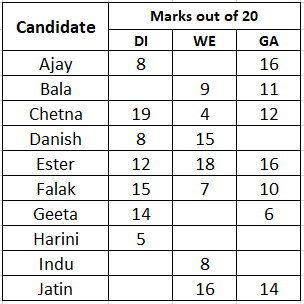
If all the candidates except Ajay and Danish had different marks in DI, and Bala's composite score was less than Chetna's composite score, then what is the maximum marks that Bala could have scored in DI?
Correct Answer: 13
It is given that Indu and Jatin both scored 100% in exactly one section. We can say that Jatin scored 100% marks in DI. Therefore, Jatin's composite score = 2*20+16+14 = 70
It is given that Jatin’s composite score was 10 more than Indu’s. Therefore, we can say that Indu's composite score = 70 - 10 = 60.
Indu also scored 100% in exactly one section.
Case 1: Indu scored 100% marks in DI.
If Indu scored 100% marks in DI, then Indu's score in GA = 60 - 2*20 - 8 = 12 which is less than 70% of maximum possible marks. Indu already has less than 70% in WE, therefore we Indu can't be recruited . Hence, we can reject this case.
Consequently, we can say that Indu scored 100% marks in WE. Therefore, Indu's score in DI = $$\dfrac{60-8-20}{2}$$ = 16
It is also given that Danish, Harini, and Indu had scored the same marks the in GA.
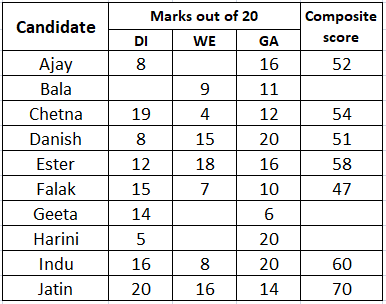
We are given that, among the four recruited, Geeta had the lowest composite score.
Maximum composite score that Geeta can get = 2*14 + 6 + 20 = 54 {Assuming 100% marks in WE}. Since, Geeta was recruitedat a composite score of 54 or less we can say that Ester was definitely recruited.
It is given that no two candidates had the same composite score. We can see that Chetna's composite score is 54. Hence, Geeta can't have a composite score of 54. Therefore, we can say that Geeta's composite score is 53 or less.
We already know the four people(Jatin, Indu, Geeta, Ester) which were recruited. Hence, we cab say that Danish was rejected at a composite score of 51. Hence, we can say that Geeta's composite score in 52 or more.
Consequently, we can say that Geeta's composite score if either 52 or 53. Therefore we can say that Geeta scored either 18 {52-(2*14+6)} or 19 {53-(2*14+6)} marks in WE.
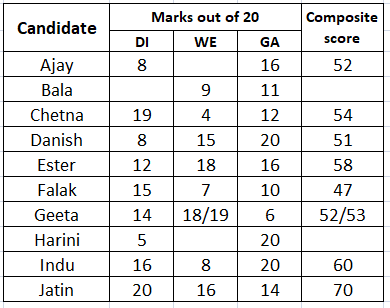
Ajay was the unique highest scorer in WE.
Case 1: Geeta scored 19 marks in WE.
We can say that if Geeta scored 19 marks in WE, then Ajay scored 20 marks in DI. In that case Ajay's composite score = 2*8 + 20 + 16 = 52. Which is a possible case.
Case 1: Geeta scored 18 marks in WE.
We can say that if Geeta scored 18 marks in WE, then Ajay can score either 19 or 20 marks in DI.
If Ajay scored 20 marks in DI then in that case Ajay's composite score = 2*8 + 20 + 16 = 52 which will be same as Geeta's composite score. Hence, we can say that in this case Ajay can't score 20 marks.
If Ajay scored 19 marks in DI then in that case Ajay's composite score = 2*8 + 19 + 16 = 51 which will be same as Danish's composite score. Hence, we can say that in this case Ajay can't score 19 marks.
Therefore, we can say that case 2 is not possible at all.
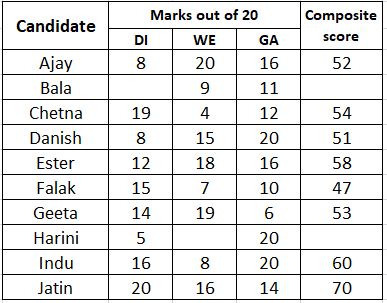
It is given that all the candidates except Ajay and Danish had different marks in DI and Bala's composite score was less than Chetna's composite score.
Let us assume that Bala scored 'x' marks in DI.
$$\Rightarrow$$ 2*x + 9 + 11 < 54
$$\Rightarrow$$ x < 17
We can see that Bala's score will be less than 17. Bala's maximum score in DI will be the largest possibel number less than 17 which is not same as any other candidate's score in DI. From, the table we can see that 16, 15 and 14 are already taken by Indu, Falak and Geeta respectively.
Therefore, we can say that Bala can score a maximum of 13 marks in DI.
Video Solution
Create a FREE account and get:
- All Quant CAT complete Formulas and shortcuts PDF
- 35+ CAT previous year papers with video solutions PDF
- 5000+ Topic-wise Previous year CAT Solved Questions for Free
