If the number of satellites serving at least two among B, C, and S is 1200, which of the following MUST be FALSE?

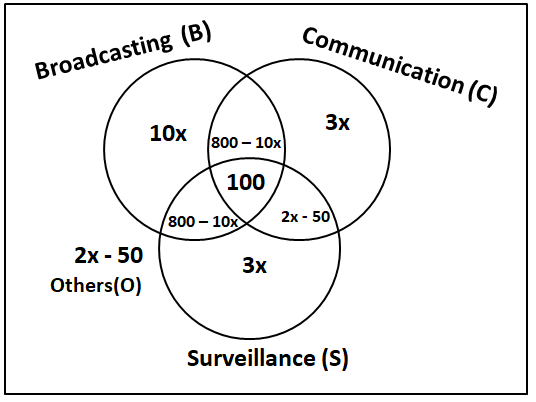
It is given that a satellite serving either B, or C, or S does not serve O. So we can say that it's basically 3 satellites broadcasting (B), communication (C), surveillance (S) which can have intersections. Those satellites which are not part of any category are placed in others. We can draw the Venn diagram as follows. 

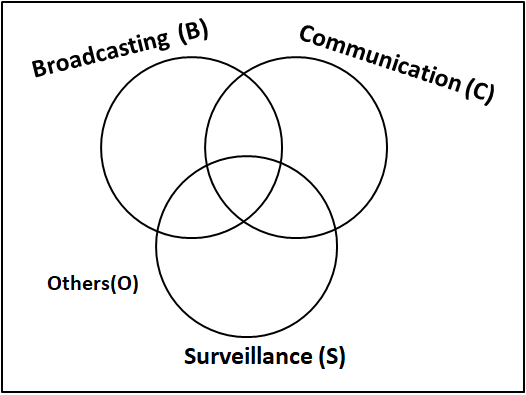
1. The numbers of satellites serving B, C, and S (though may be not exclusively) are in the ratio 2:1:1. 2. The number of satellites serving all three of B, C, and S is 100. 3. The number of satellites exclusively serving C is the same as the number of satellites exclusively serving S. This number is 30% of the number of satellites exclusively serving B. 4. The number of satellites serving O is the same as the number of satellites serving both C and S but not B.

Let '10x' be the number of satellites exclusively serving B. Then, the number of satellites exclusively serving C and S = 0.30*10x = 3x

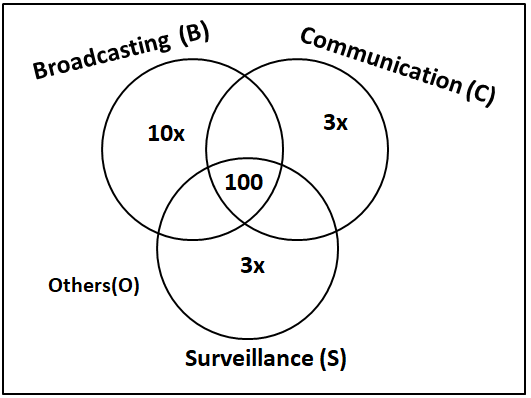
Let 'y' be the number of satellites serving others(O).

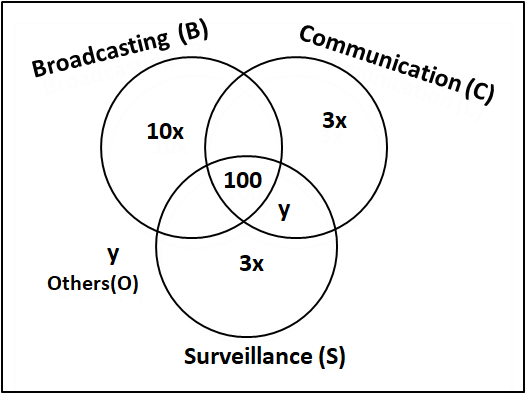
Let 'z' be the number of satellites serving B, C but not S. Since the numbers of satellites serving B, C, and S (though may be not exclusively) are in the ratio 2:1:1. Therefore, we can can say that number of satellites serving B, S but not C = z.

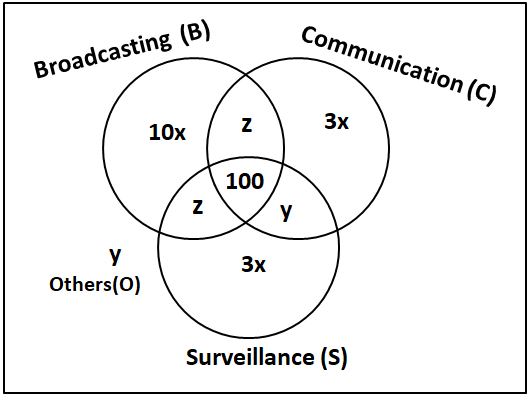
It is given that 

$$\Rightarrow$$ 10x+2z+2y+6x+100 = 1600

$$\Rightarrow$$ 8x+z+y = 750 ... (1)

The numbers of satellites serving B, C, and S (though may be not exclusively) are in the ratio 2:1:1.

$$\Rightarrow$$ $$\dfrac{10x+2z+100}{z+100+3x+y} = \dfrac{2}{1}$$

$$\Rightarrow$$ $$10x+2z+100=2(z+100+3x+y)$$

$$\Rightarrow$$ $$4x=100+2y$$

$$\Rightarrow$$ $$2x=50+y$$

$$\Rightarrow$$ $$y=2x-50$$   ... (2)

We can substitute this in equation (1)

$$\Rightarrow$$ 8x+z+2x - 50 = 750

$$\Rightarrow$$ z = 800 - 10x    ... (3)

Let us define boundary condition for x, 

$$\Rightarrow$$ 2x - 50 $$\geq$$ 0

$$\Rightarrow$$ x $$\geq$$ 25

Also,  800 - 10x $$\geq$$ 0

$$\Rightarrow$$ x $$\leq$$ 80

Therefore, we can say that x $$\epsilon$$ [25, 80].

It is given that the number of satellites serving at least two among B, C, and S is 1200.

$$\Rightarrow$$ 800 - 10x + 800 - 10x + 2x -50 + 100 = 1200

$$\Rightarrow$$ 18x = 450

$$\Rightarrow$$ x = 25

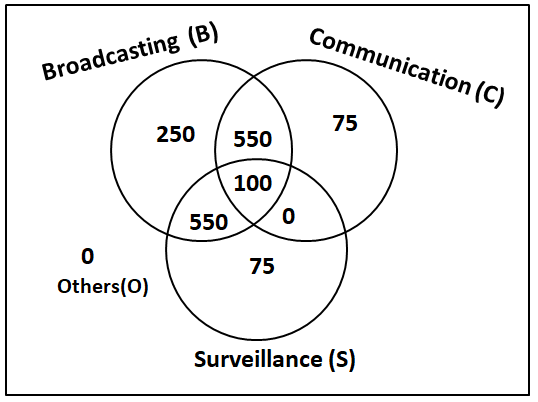
We can determine number of satellites in each of the following category. Hence, option C is definitely false. Therefore, we can say that option C is incorrect.