Please enter the following details
Twenty four people are part of three committees which are to look at research, teaching, and administration respectively. No two committees have any member in common. No two committees are of the same size. Each committee has three types of people: bureaucrats, educationalists, and politicians, with at least one from each of the three types in each committee. The following facts are also known about the committees:
1. The numbers of bureaucrats in the research and teaching committees are equal, while the number of bureaucrats in the research committee is 75% of the number of bureaucrats in the administration committee.
2. The number of educationalists in the teaching committee is less than the number of educationalists in the research committee. The number of educationalists in the research committee is the average of the numbers of educationalists in the other two committees.
3. 60% of the politicians are in the administration committee, and 20% are in the teaching committee.
Which of the following CANNOT be determined uniquely based on the given information?
Let us draw a table according to the information given.
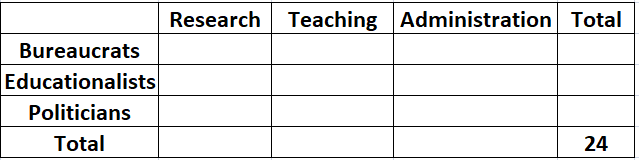
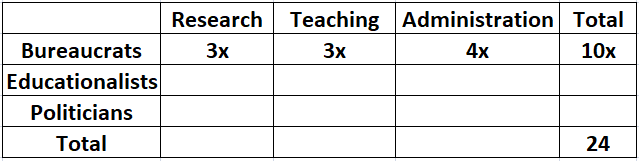
It is given that the numbers of bureaucrats in the research and teaching committees are equal, while the number of bureaucrats in the research committee is 75% of the number of bureaucrats in the administration committee. Let '4x' be the number of bureaucrats in Administration committee.
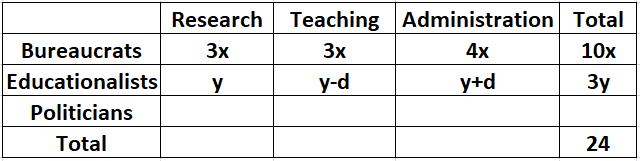
The number of educationalists in the teaching committee is less than the number of educationalists in the research committee. The number of educationalists in the research committee is the average of the numbers of educationalists in the other two committees. Let us assume that 'y' is the number of educationalists in the research committee and 'd' be the difference in the number of educationalists in Research and teaching committees.
60% of the politicians are in the administration committee, and 20% are in the teaching committee. Let '5z' be the number of total number of politicians.
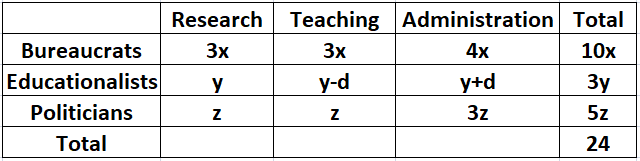
We can say that
$$\Rightarrow$$ 10x+3y+5z = 24
We can see that each of x, y and z has to a natural number integer. If x > 1, then both y and z can't take any natural number.
Hence, we can say that x = 1.
At x = 1, 3y+5z = 14. If y = 1 or 2, Z is not an integer.
At x = 1 and y = 3, z = 1 which is the only possible solution.
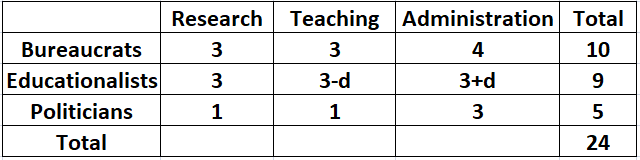
We can see that 'd' can assume two possible values. d = 1 or 2.
From the table, we can not uniquely determine the size of the teaching committee. Hence, option A is the correct answer.
Video Solution
Create a FREE account and get:
- All Quant CAT complete Formulas and shortcuts PDF
- 35+ CAT previous year papers with video solutions PDF
- 5000+ Topic-wise Previous year CAT Solved Questions for Free
