You are given an n×n square matrix to be filled with numerals so that no two adjacent cells have the same numeral. Two cells are called adjacent if they touch each other horizontally, vertically or diagonally. So a cell in one of the four corners has three cells adjacent to it, and a cell in the first or last row or column which is not in the corner has five cells adjacent to it. Any other cell has eight cells adjacent to it.
What is the minimum number of different numerals needed to fill a 3×3 square matrix?
Correct Answer: 4
Let us use 1 to denote the first number that we fill. We have to fill as many squares with 1 as possible. If we start with the top-left square, we can fill 4 squares with the number 1.
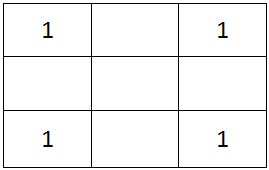
Now, we can fill number 2 only in 2 of the 5 squares available.
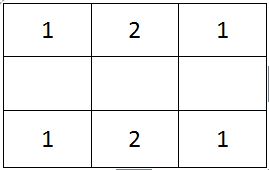
The 3 squares available now are adjacent to each other. Therefore, we will require at least 2 numbers to fill these squares.
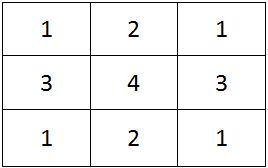
We need a minimum of 4 numbers to fill a 3x3 square matrix such that no 2 adjacent cells contain the same number. Therefore, 4 is the correct answer.
Video Solution
Create a FREE account and get:
- All Quant CAT complete Formulas and shortcuts PDF
- 35+ CAT previous papers with video solutions PDF
- 5000+ Topic-wise Previous year CAT Solved Questions for Free
