CAT 2000 Question Paper
For the following questions answer them individually
CAT 2000 - Question 151
If a,b,c are the sides of a triangle, and $$a^2 + b^2 +c^2 = bc + ca + ab$$, then the triangle is:
CAT 2000 - Question 152
In the figure AB=BC=CD=DE=EF=FG=GA, then $$\angle{DAE}$$ is approximately
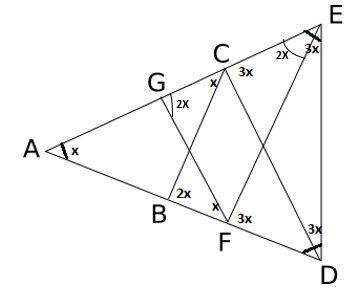
CAT 2000 - Question 153
A shipping clerk has five boxes of different but unknown weights each weighing less than 100 kgs. The clerk weighs the boxes in pairs. The weights obtained are 110, 112, 113, 114, 115, 116, 117, 118, 120 and 121 kgs. What is the weight, in kgs, of the heaviest box?
CAT 2000 - Question 154
There are three cities A, B and C. Each of these cities is connected with the other two cities by at least one direct road. If a traveller wants to go from one city (origin) to another city (destination), she can do so either by traversing a road connecting the two cities directly, or by traversing two roads, the, first connecting the origin to the third city and the second connecting the third city to the destination. In all there are 33 routes from A to B (including those via C). Similarly there are 23 routes from B to C (including those via A). How many roads are there from A to C directly?
CAT 2000 - Question 155
The set of all positive integers is the union of two disjoint subsets:
{f(1), f(2),.....f(n), ...} and {g(1),g(2).... ,g(n).....}, where f(1) < f(2) <.....< f(n)..., and g(1) < g(2) < ..... < g(n) ...,and
g(n) = f(f(n))+1 for all n >= 1. What is the value of g(1)?
CAT 2000 - Question 156
ABCDEFGH is a regular octagon. A and E are opposite vertices of the octagon. A frog starts jumping from vertex to vertex, beginning from A. From any vertex of the octagon except E, it may jump to either of the two adjacent vertices. When it reaches E, the frog stops and says there. Let $$a_n$$ be the number of distinct paths of exactly n jumps ending in E. Then, what is the value of $$a_{2n-1}$$?
CAT 2000 - Question 157
For all non-negative integers x and y, f(x, y) is defined as below:
f(0, y) = y + 1
f(x + 1, 0) = f(x, 1)
f(x+ 1, y+ 1)= f(x, f(x+ 1, y))
Then, what is the value of f(1,2)?
CAT 2000 - Question 158
Convert the number 1982 from base 10 to base 12. The result is:
CAT 2000 - Question 159
Two full tanks, one shaped like a cylinder and the other like a cone, contain jet fuel. The cylindrical tank holds 500 litres more than the conical tank. After 200 litres of fuel has been pumped out from each tank the cylindrical tank contains twice the amount of fuel in the conical tank. How many litres of fuel did the cylindrical tank have when it was full?
CAT 2000 - Question 160
A farmer has decided to build a wire fence along one straight side of this property. For this, he planned to place several fence-posts at six metre intervals, with posts fixed at both ends of the side. After he bought the posts and wire, he found that the number of posts he had bought was five less than required. However, he discovered that the number of posts he had bought would be just sufficient if he spaced them eight metres apart. What is the length of the side of his property and how many posts did he buy?
Two Factor Authentication
Incase of any issue contact support@cracku.in