Top 55 CAT Puzzles Questions PDF With Video Solutions
Puzzles are an important topic in the CAT Logical Reasoning & Data Interpretation (LRDI) Section. Usually, the Sets on Puzzles are not very tough to crack and hence one must not miss out on the LRDI Sets on Puzzles. You can check out these Puzzles questions from the CAT Previous year's papers. Practice a good number of sums on CAT Puzzle questions so that you can answer these questions with ease in the exam. In this article, we will look into some important Puzzle Questions for CAT LRDI. These are a good source for practice; If you want to practice these questions, you can download this Important CAT Puzzle Questions PDF below, which is completely Free.
Note: No Sign-Up is required to download the PDF
CAT Puzzles Weightage Over Past 5 Years
Year | Weightage |
| 2024 | 10 |
| 2023 | 10 |
2022 | 12 |
2021 | 8 |
| 2020 | 8 |
CAT 2024 Puzzles questions
The numbers 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10 are placed in ten slots of the following grid based on the conditions below.
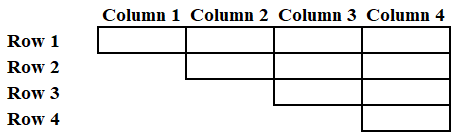
1. Numbers in any row appear in an increasing order from left to right.
2. Numbers in any column appear in a decreasing order from top to bottom.
3. 1 is placed either in the same row or in the same column as 10.
4. Neither 2 nor 3 is placed in the same row or in the same column as 10.
5. Neither 7 nor 8 is placed in the same row or in the same column as 9.
6. 4 and 6 are placed in the same row.
Question 1
What is the row number which has the least sum of numbers placed in that row?
correct answer:-4
Instruction for set 1:
The numbers 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10 are placed in ten slots of the following grid based on the conditions below.

1. Numbers in any row appear in an increasing order from left to right.
2. Numbers in any column appear in a decreasing order from top to bottom.
3. 1 is placed either in the same row or in the same column as 10.
4. Neither 2 nor 3 is placed in the same row or in the same column as 10.
5. Neither 7 nor 8 is placed in the same row or in the same column as 9.
6. 4 and 6 are placed in the same row.
Question 2
Which of the following statements MUST be true?
I. 10 is placed in a slot in Row 1.
II. 1 is placed in a slot in Row 4.
correct answer:-1
Instruction for set 1:
The numbers 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10 are placed in ten slots of the following grid based on the conditions below.

1. Numbers in any row appear in an increasing order from left to right.
2. Numbers in any column appear in a decreasing order from top to bottom.
3. 1 is placed either in the same row or in the same column as 10.
4. Neither 2 nor 3 is placed in the same row or in the same column as 10.
5. Neither 7 nor 8 is placed in the same row or in the same column as 9.
6. 4 and 6 are placed in the same row.
Question 3
Which of the following statements MUST be true?
I. 2 is placed in a slot in Column 2.
II. 3 is placed in a slot in Column 3.
correct answer:-3
Instruction for set 1:
The numbers 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10 are placed in ten slots of the following grid based on the conditions below.

1. Numbers in any row appear in an increasing order from left to right.
2. Numbers in any column appear in a decreasing order from top to bottom.
3. 1 is placed either in the same row or in the same column as 10.
4. Neither 2 nor 3 is placed in the same row or in the same column as 10.
5. Neither 7 nor 8 is placed in the same row or in the same column as 9.
6. 4 and 6 are placed in the same row.
Question 4
For how many slots in the grid, placement of numbers CANNOT be determined with certainty?
correct answer:-2
Instruction for set 1:
The numbers 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10 are placed in ten slots of the following grid based on the conditions below.

1. Numbers in any row appear in an increasing order from left to right.
2. Numbers in any column appear in a decreasing order from top to bottom.
3. 1 is placed either in the same row or in the same column as 10.
4. Neither 2 nor 3 is placed in the same row or in the same column as 10.
5. Neither 7 nor 8 is placed in the same row or in the same column as 9.
6. 4 and 6 are placed in the same row.
Question 5
What is the sum of the numbers placed in Column 4?
correct answer:-26
Instruction for set 2:
Eight gymnastics players numbered 1 through 8 underwent a training camp where they were coached by three coaches - Xena, Yuki, and Zara. Each coach trained at least two players. Yuki trained only even numbered players, while Zara trained only odd numbered players. After the camp, the coaches evaluated the players and gave integer ratings to the respective players trained by them on a scale of 1 to 7, with 1 being the lowest rating and 7 the highest.
The following additional information is known.
1. Xena trained more players than Yuki.
2. Player-1 and Player-4 were trained by the same coach, while the coaches who trained Player-2, Player-3 and Player-5 were all different.
3. Player-5 and Player-7 were trained by the same coach and got the same rating. All other players got a unique rating.
4. The average of the ratings of all the players was 4.
5. Player-2 got the highest rating.
6. The average of the ratings of the players trained by Yuki was twice that of the players trained by Xena and two more than that of the players trained by Zara.
7. Player-4's rating was double of Player-8's and less than Player-5's.
Question 6
What best can be concluded about the number of players coached by Zara?
correct answer:-2
Instruction for set 2:
Eight gymnastics players numbered 1 through 8 underwent a training camp where they were coached by three coaches - Xena, Yuki, and Zara. Each coach trained at least two players. Yuki trained only even numbered players, while Zara trained only odd numbered players. After the camp, the coaches evaluated the players and gave integer ratings to the respective players trained by them on a scale of 1 to 7, with 1 being the lowest rating and 7 the highest.
The following additional information is known.
1. Xena trained more players than Yuki.
2. Player-1 and Player-4 were trained by the same coach, while the coaches who trained Player-2, Player-3 and Player-5 were all different.
3. Player-5 and Player-7 were trained by the same coach and got the same rating. All other players got a unique rating.
4. The average of the ratings of all the players was 4.
5. Player-2 got the highest rating.
6. The average of the ratings of the players trained by Yuki was twice that of the players trained by Xena and two more than that of the players trained by Zara.
7. Player-4's rating was double of Player-8's and less than Player-5's.
Question 7
What was the rating of Player-7?
correct answer:-4
Instruction for set 2:
Eight gymnastics players numbered 1 through 8 underwent a training camp where they were coached by three coaches - Xena, Yuki, and Zara. Each coach trained at least two players. Yuki trained only even numbered players, while Zara trained only odd numbered players. After the camp, the coaches evaluated the players and gave integer ratings to the respective players trained by them on a scale of 1 to 7, with 1 being the lowest rating and 7 the highest.
The following additional information is known.
1. Xena trained more players than Yuki.
2. Player-1 and Player-4 were trained by the same coach, while the coaches who trained Player-2, Player-3 and Player-5 were all different.
3. Player-5 and Player-7 were trained by the same coach and got the same rating. All other players got a unique rating.
4. The average of the ratings of all the players was 4.
5. Player-2 got the highest rating.
6. The average of the ratings of the players trained by Yuki was twice that of the players trained by Xena and two more than that of the players trained by Zara.
7. Player-4's rating was double of Player-8's and less than Player-5's.
Question 8
What was the rating of Player-6?
correct answer:-5
Instruction for set 2:
Eight gymnastics players numbered 1 through 8 underwent a training camp where they were coached by three coaches - Xena, Yuki, and Zara. Each coach trained at least two players. Yuki trained only even numbered players, while Zara trained only odd numbered players. After the camp, the coaches evaluated the players and gave integer ratings to the respective players trained by them on a scale of 1 to 7, with 1 being the lowest rating and 7 the highest.
The following additional information is known.
1. Xena trained more players than Yuki.
2. Player-1 and Player-4 were trained by the same coach, while the coaches who trained Player-2, Player-3 and Player-5 were all different.
3. Player-5 and Player-7 were trained by the same coach and got the same rating. All other players got a unique rating.
4. The average of the ratings of all the players was 4.
5. Player-2 got the highest rating.
6. The average of the ratings of the players trained by Yuki was twice that of the players trained by Xena and two more than that of the players trained by Zara.
7. Player-4's rating was double of Player-8's and less than Player-5's.
Question 9
For how many players the ratings can be determined with certainty?
correct answer:-6
Instruction for set 2:
Eight gymnastics players numbered 1 through 8 underwent a training camp where they were coached by three coaches - Xena, Yuki, and Zara. Each coach trained at least two players. Yuki trained only even numbered players, while Zara trained only odd numbered players. After the camp, the coaches evaluated the players and gave integer ratings to the respective players trained by them on a scale of 1 to 7, with 1 being the lowest rating and 7 the highest.
The following additional information is known.
1. Xena trained more players than Yuki.
2. Player-1 and Player-4 were trained by the same coach, while the coaches who trained Player-2, Player-3 and Player-5 were all different.
3. Player-5 and Player-7 were trained by the same coach and got the same rating. All other players got a unique rating.
4. The average of the ratings of all the players was 4.
5. Player-2 got the highest rating.
6. The average of the ratings of the players trained by Yuki was twice that of the players trained by Xena and two more than that of the players trained by Zara.
7. Player-4's rating was double of Player-8's and less than Player-5's.
Question 10
Who all were the players trained by Xena?
correct answer:-2
CAT 2023 Puzzles questions
Faculty members in a management school can belong to one of four departments - Finance and Accounting (F&A), Marketing and Strategy (M&S), Operations and Quants (O&Q) and Behaviour and Human Resources (B&H). The numbers of faculty members in F&A, M&S, O&Q and B&H departments are 9, 7, 5 and 3 respectively.
Prof. Pakrasi, Prof. Qureshi, Prof. Ramaswamy and Prof. Samuel are four members of the school's faculty who were candidates for the post of the Dean of the school. Only one of the candidates was from O&Q.
Every faculty member, including the four candidates, voted for the post. In each department, all the faculty members who were not candidates voted for the same candidate. The rules for the election are listed below.
1. There cannot be more than two candidates from a single department.
2. A candidate cannot vote for himself/herself.
3. Faculty members cannot vote for a candidate from their own department.
After the election, it was observed that Prof. Pakrasi received 3 votes, Prof. Qureshi received 14 votes, Prof. Ramaswamy received 6 votes and Prof. Samuel received 1 vote. Prof. Pakrasi voted for Prof. Ramaswamy, Prof. Qureshi for Prof. Samuel, Prof. Ramaswamy for Prof. Qureshi and Prof. Samuel for Prof. Pakrasi.
Question 1
Which two candidates can belong to the same department?
correct answer:-1
Instruction for set 1:
Faculty members in a management school can belong to one of four departments - Finance and Accounting (F&A), Marketing and Strategy (M&S), Operations and Quants (O&Q) and Behaviour and Human Resources (B&H). The numbers of faculty members in F&A, M&S, O&Q and B&H departments are 9, 7, 5 and 3 respectively.
Prof. Pakrasi, Prof. Qureshi, Prof. Ramaswamy and Prof. Samuel are four members of the school's faculty who were candidates for the post of the Dean of the school. Only one of the candidates was from O&Q.
Every faculty member, including the four candidates, voted for the post. In each department, all the faculty members who were not candidates voted for the same candidate. The rules for the election are listed below.
1. There cannot be more than two candidates from a single department.
2. A candidate cannot vote for himself/herself.
3. Faculty members cannot vote for a candidate from their own department.
After the election, it was observed that Prof. Pakrasi received 3 votes, Prof. Qureshi received 14 votes, Prof. Ramaswamy received 6 votes and Prof. Samuel received 1 vote. Prof. Pakrasi voted for Prof. Ramaswamy, Prof. Qureshi for Prof. Samuel, Prof. Ramaswamy for Prof. Qureshi and Prof. Samuel for Prof. Pakrasi.
Question 2
Which of the following can be the number of votes that Prof. Qureshi received from a single department?
correct answer:-4
Instruction for set 1:
Faculty members in a management school can belong to one of four departments - Finance and Accounting (F&A), Marketing and Strategy (M&S), Operations and Quants (O&Q) and Behaviour and Human Resources (B&H). The numbers of faculty members in F&A, M&S, O&Q and B&H departments are 9, 7, 5 and 3 respectively.
Prof. Pakrasi, Prof. Qureshi, Prof. Ramaswamy and Prof. Samuel are four members of the school's faculty who were candidates for the post of the Dean of the school. Only one of the candidates was from O&Q.
Every faculty member, including the four candidates, voted for the post. In each department, all the faculty members who were not candidates voted for the same candidate. The rules for the election are listed below.
1. There cannot be more than two candidates from a single department.
2. A candidate cannot vote for himself/herself.
3. Faculty members cannot vote for a candidate from their own department.
After the election, it was observed that Prof. Pakrasi received 3 votes, Prof. Qureshi received 14 votes, Prof. Ramaswamy received 6 votes and Prof. Samuel received 1 vote. Prof. Pakrasi voted for Prof. Ramaswamy, Prof. Qureshi for Prof. Samuel, Prof. Ramaswamy for Prof. Qureshi and Prof. Samuel for Prof. Pakrasi.
Question 3
If Prof. Samuel belongs to B&H, which of the following statements is/are true?
Statement A: Prof. Pakrasi belongs to M&S.
Statement B: Prof. Ramaswamy belongs to O&Q
correct answer:-4
Instruction for set 1:
Faculty members in a management school can belong to one of four departments - Finance and Accounting (F&A), Marketing and Strategy (M&S), Operations and Quants (O&Q) and Behaviour and Human Resources (B&H). The numbers of faculty members in F&A, M&S, O&Q and B&H departments are 9, 7, 5 and 3 respectively.
Prof. Pakrasi, Prof. Qureshi, Prof. Ramaswamy and Prof. Samuel are four members of the school's faculty who were candidates for the post of the Dean of the school. Only one of the candidates was from O&Q.
Every faculty member, including the four candidates, voted for the post. In each department, all the faculty members who were not candidates voted for the same candidate. The rules for the election are listed below.
1. There cannot be more than two candidates from a single department.
2. A candidate cannot vote for himself/herself.
3. Faculty members cannot vote for a candidate from their own department.
After the election, it was observed that Prof. Pakrasi received 3 votes, Prof. Qureshi received 14 votes, Prof. Ramaswamy received 6 votes and Prof. Samuel received 1 vote. Prof. Pakrasi voted for Prof. Ramaswamy, Prof. Qureshi for Prof. Samuel, Prof. Ramaswamy for Prof. Qureshi and Prof. Samuel for Prof. Pakrasi.
Question 4
What best can be concluded about the candidate from O&Q?
correct answer:-2
Instruction for set 1:
Faculty members in a management school can belong to one of four departments - Finance and Accounting (F&A), Marketing and Strategy (M&S), Operations and Quants (O&Q) and Behaviour and Human Resources (B&H). The numbers of faculty members in F&A, M&S, O&Q and B&H departments are 9, 7, 5 and 3 respectively.
Prof. Pakrasi, Prof. Qureshi, Prof. Ramaswamy and Prof. Samuel are four members of the school's faculty who were candidates for the post of the Dean of the school. Only one of the candidates was from O&Q.
Every faculty member, including the four candidates, voted for the post. In each department, all the faculty members who were not candidates voted for the same candidate. The rules for the election are listed below.
1. There cannot be more than two candidates from a single department.
2. A candidate cannot vote for himself/herself.
3. Faculty members cannot vote for a candidate from their own department.
After the election, it was observed that Prof. Pakrasi received 3 votes, Prof. Qureshi received 14 votes, Prof. Ramaswamy received 6 votes and Prof. Samuel received 1 vote. Prof. Pakrasi voted for Prof. Ramaswamy, Prof. Qureshi for Prof. Samuel, Prof. Ramaswamy for Prof. Qureshi and Prof. Samuel for Prof. Pakrasi.
Question 5
Which of the following statements is/are true?
Statement A: Non-candidates from M&S voted for Prof. Qureshi.
Statement B: Non-candidates from F&A voted for Prof. Qureshi.
correct answer:-2
Instruction for set 2:
Anjali, Bipasha, and Chitra visited an entertainment park that has four rides. Each ride lasts one hour and can accommodate one visitor at one point. All rides begin at 9 am and must be completed by 5 pm except for Ride-3, for which the last ride has to be completed by 1 pm. Ride gates open every 30 minutes, e.g. 10 am, 10:30 am, and so on. Whenever a ride gate opens, and there is no visitor inside, the first visitor waiting in the queue buys the ticket just before taking the ride. The ticket prices are Rs. 20, Rs. 50, Rs. 30 and Rs. 40 for Rides 1 to 4, respectively. Each of the three visitors took at least one ride and did not necessarily take all rides. None of them took the same ride more than once. The movement time from one ride to another is negligible, and a visitor leaves the ride immediately after the completion of the ride. No one takes a break inside the park unless mentioned explicitly.
The following information is also known.
1. Chitra never waited in the queue and completed her visit by 11 am after spending Rs. 50 to pay for the ticket(s).
2. Anjali took Ride-1 at 11 am after waiting for 30 mins for Chitra to complete it. It was the only ride where Anjali waited.
3. Bipasha began her first of three rides at 11:30 am. All three visitors incurred the same amount of ticket expense by 12:15 pm.
4. The last ride taken by Anjali and Bipasha was the same, where Bipasha waited 30 mins for Anjali to complete her ride. Before standing in the queue for that ride, Bipasha took a 1-hour coffee break after completing her previous ride.
Question 6
What was the total amount spent on tickets (in Rs.) by Bipasha?
correct answer:-3
Instruction for set 2:
Anjali, Bipasha, and Chitra visited an entertainment park that has four rides. Each ride lasts one hour and can accommodate one visitor at one point. All rides begin at 9 am and must be completed by 5 pm except for Ride-3, for which the last ride has to be completed by 1 pm. Ride gates open every 30 minutes, e.g. 10 am, 10:30 am, and so on. Whenever a ride gate opens, and there is no visitor inside, the first visitor waiting in the queue buys the ticket just before taking the ride. The ticket prices are Rs. 20, Rs. 50, Rs. 30 and Rs. 40 for Rides 1 to 4, respectively. Each of the three visitors took at least one ride and did not necessarily take all rides. None of them took the same ride more than once. The movement time from one ride to another is negligible, and a visitor leaves the ride immediately after the completion of the ride. No one takes a break inside the park unless mentioned explicitly.
The following information is also known.
1. Chitra never waited in the queue and completed her visit by 11 am after spending Rs. 50 to pay for the ticket(s).
2. Anjali took Ride-1 at 11 am after waiting for 30 mins for Chitra to complete it. It was the only ride where Anjali waited.
3. Bipasha began her first of three rides at 11:30 am. All three visitors incurred the same amount of ticket expense by 12:15 pm.
4. The last ride taken by Anjali and Bipasha was the same, where Bipasha waited 30 mins for Anjali to complete her ride. Before standing in the queue for that ride, Bipasha took a 1-hour coffee break after completing her previous ride.
Question 7
Which were all the rides that Anjali completed by 2:00 pm?
correct answer:-2
Instruction for set 2:
Anjali, Bipasha, and Chitra visited an entertainment park that has four rides. Each ride lasts one hour and can accommodate one visitor at one point. All rides begin at 9 am and must be completed by 5 pm except for Ride-3, for which the last ride has to be completed by 1 pm. Ride gates open every 30 minutes, e.g. 10 am, 10:30 am, and so on. Whenever a ride gate opens, and there is no visitor inside, the first visitor waiting in the queue buys the ticket just before taking the ride. The ticket prices are Rs. 20, Rs. 50, Rs. 30 and Rs. 40 for Rides 1 to 4, respectively. Each of the three visitors took at least one ride and did not necessarily take all rides. None of them took the same ride more than once. The movement time from one ride to another is negligible, and a visitor leaves the ride immediately after the completion of the ride. No one takes a break inside the park unless mentioned explicitly.
The following information is also known.
1. Chitra never waited in the queue and completed her visit by 11 am after spending Rs. 50 to pay for the ticket(s).
2. Anjali took Ride-1 at 11 am after waiting for 30 mins for Chitra to complete it. It was the only ride where Anjali waited.
3. Bipasha began her first of three rides at 11:30 am. All three visitors incurred the same amount of ticket expense by 12:15 pm.
4. The last ride taken by Anjali and Bipasha was the same, where Bipasha waited 30 mins for Anjali to complete her ride. Before standing in the queue for that ride, Bipasha took a 1-hour coffee break after completing her previous ride.
Question 8
Which ride was taken by all three visitors?
correct answer:-1
Instruction for set 2:
Anjali, Bipasha, and Chitra visited an entertainment park that has four rides. Each ride lasts one hour and can accommodate one visitor at one point. All rides begin at 9 am and must be completed by 5 pm except for Ride-3, for which the last ride has to be completed by 1 pm. Ride gates open every 30 minutes, e.g. 10 am, 10:30 am, and so on. Whenever a ride gate opens, and there is no visitor inside, the first visitor waiting in the queue buys the ticket just before taking the ride. The ticket prices are Rs. 20, Rs. 50, Rs. 30 and Rs. 40 for Rides 1 to 4, respectively. Each of the three visitors took at least one ride and did not necessarily take all rides. None of them took the same ride more than once. The movement time from one ride to another is negligible, and a visitor leaves the ride immediately after the completion of the ride. No one takes a break inside the park unless mentioned explicitly.
The following information is also known.
1. Chitra never waited in the queue and completed her visit by 11 am after spending Rs. 50 to pay for the ticket(s).
2. Anjali took Ride-1 at 11 am after waiting for 30 mins for Chitra to complete it. It was the only ride where Anjali waited.
3. Bipasha began her first of three rides at 11:30 am. All three visitors incurred the same amount of ticket expense by 12:15 pm.
4. The last ride taken by Anjali and Bipasha was the same, where Bipasha waited 30 mins for Anjali to complete her ride. Before standing in the queue for that ride, Bipasha took a 1-hour coffee break after completing her previous ride.
Question 9
How many rides did Anjali and Chitra take in total?
correct answer:-6
Instruction for set 2:
Anjali, Bipasha, and Chitra visited an entertainment park that has four rides. Each ride lasts one hour and can accommodate one visitor at one point. All rides begin at 9 am and must be completed by 5 pm except for Ride-3, for which the last ride has to be completed by 1 pm. Ride gates open every 30 minutes, e.g. 10 am, 10:30 am, and so on. Whenever a ride gate opens, and there is no visitor inside, the first visitor waiting in the queue buys the ticket just before taking the ride. The ticket prices are Rs. 20, Rs. 50, Rs. 30 and Rs. 40 for Rides 1 to 4, respectively. Each of the three visitors took at least one ride and did not necessarily take all rides. None of them took the same ride more than once. The movement time from one ride to another is negligible, and a visitor leaves the ride immediately after the completion of the ride. No one takes a break inside the park unless mentioned explicitly.
The following information is also known.
1. Chitra never waited in the queue and completed her visit by 11 am after spending Rs. 50 to pay for the ticket(s).
2. Anjali took Ride-1 at 11 am after waiting for 30 mins for Chitra to complete it. It was the only ride where Anjali waited.
3. Bipasha began her first of three rides at 11:30 am. All three visitors incurred the same amount of ticket expense by 12:15 pm.
4. The last ride taken by Anjali and Bipasha was the same, where Bipasha waited 30 mins for Anjali to complete her ride. Before standing in the queue for that ride, Bipasha took a 1-hour coffee break after completing her previous ride.
Question 10
What was the total amount spent on tickets (in Rs.) by Anjali?
correct answer:-140

