Sixteen patients in a hospital must undergo a blood test for a disease. It is known that exactly one of them has the disease. The hospital has only eight testing kits and has decided to pool blood samples of patients into eight vials for the tests. The patients are numbered 1 through 16, and the vials are labelled A, B, C, D, E, F, G, and H. The following table shows the vials into which each patient’s blood sample is distributed.
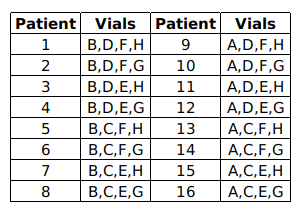
If a patient has the disease, then each vial containing his/her blood sample will test positive. If a vial tests positive, one of the patients whose blood samples were mixed in the vial has the disease. If a vial tests negative, then none of the patients whose blood samples were mixed in the vial has the disease.
Suppose one of the lab assistants accidentally mixed two patients' blood samples before they were distributed to the vials. Which of the following correctly represents the set of all possible numbers of positive test results out of the eight vials?
Let one of the patients, patient 1 or patient 16 has the disease and his blood is mixed with other them all 8 vials will tests positive. ⇒
8 has to be one of the answers.
If patient 2 and patients 16’s blood is mixed of one of them has the disease then 7 of the 8 vials will test positive. So 7 has to be there in the option.
If 1 has the disease and 1, 7 are mixed then 6 out the 8 vials tests positive.
IF 1 has the disease and 1,9 are mixed then 5 of the 8 vials tests positive,
Now, let us assume that patient 1 has the disease if his blood is not mixed,
then 4 vials will definitely show positive.
Hence 3 is the correct answer.
Video Solution

Your Doubts
Create a FREE account and get:
- All Quant CAT complete Formulas and shortcuts PDF
- 38+ CAT previous year papers with video solutions PDF
- 5000+ Topic-wise Previous year CAT Solved Questions for Free





