CMAT 2025 Slot 1 Question Paper
Study the given pie charts carefully to answer the questions that follows.
Comprehension:
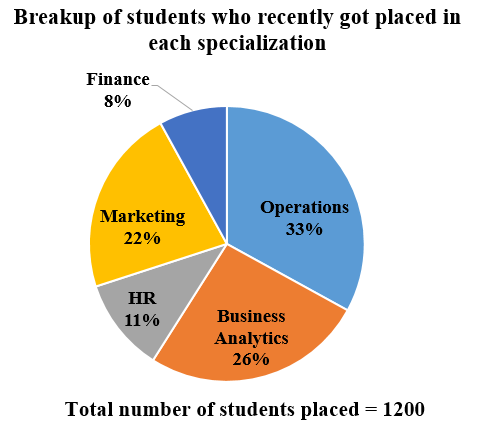
Break up of number of students studying in different specialization of management college and the number of students who recently got placed in each specialization.
The total number of students who got placed from all the specialization together was what percentage of total number of students pursuing specialization in operations, market ing and finance collectively?
What is the difference between the total number of students pursuing specialization in Business Analytics and HR combined and the number of student who got placed from marketing specialization and finance specialization combined?
The number of students who got placed from the HR specialization was what percent of the total number of students studying in that specialization?
For the following questions answer them individually
Arrange the following in descending order
(A) $$3^{3^{3^{3}}}$$
(B) $$3^{(33)^{3}}$$
(C) $$(3^3)^{33}$$
(D) $$3^{333}$$
Choose the correct answer from the options given below :
In a circus there were a leopard and a tiger walking in the two different rings having same radii. It was observed that when leopard moved 3 steps, tiger moved 5 steps in the same time, but the distance traversed by leopard in 5 steps is equal to the distance traversed by tiger in 4 steps. How many rounds that a leopard made t ill when tiger completed 100 rounds?
There are three bottles of mixture of syrup and water in the ratios 2 : 3, 3 : 4 and 7 : 5. 10 litres of first and 21 litres of second bottles are taken. How much quantity of mixtures from third bottle is to be taken so that the final syrup and water ratio of mixture from three bottles will be 1 : 1 if the final mixture from all the three bottles is added and mixed in a big container?
A vegetable vendor by means of his false balance defrauds to the extent of 10% in buying goods and also defrauds to 10% in selling, then the gain percent is
If $$x^2 = y + z , y^2 = z + x$$ and $$z^2 = x + y$$ then the value of $$\frac{1}{x + 1} + \frac{1}{y + 1} + \frac{1}{z + 1}$$ is
20 girls, among whom are A and B sit down at a round table. The probability that there are 4 girls between A and B is
Reema had 'n' chocolates. She distributed them among 4 children in the ratio of $$\frac{1}{2} : \frac{1}{3} : \frac{1}{5} : \frac{1}{8}$$. If she gave them each one a complete chocolate, the minimum number of chocolates she had distributed.
