CAT 2025 Slot 2 Question Paper

If m and n are integers such that $$(m+2n)(2m+n)=27$$, then the maximum possible value of $$2m-3n$$ is

The sum of digits of the number $$(625)^{65} \times (128)^{36}$$ is

The equations $$3x^{2}-5x+p=0$$ and $$2x^{2}-2x+q=0$$ have one common root. The sum of the other roots of this equations is

Tf $$\log_{64}{x^{2}+\log_{8}{\sqrt{y}+3\log_{512}{(\sqrt{y}z)}}}=4$$, where x,y and z are positive real numbers, then the minimum possible value of (x+y+z) is

Rita and Sneha can row a boat at 5 km/h and 6 km/h in still water, respectively. In a river flowing with a constant velocity, Sneha takes 48 minutes more to row 14 km upstream than to row the same distance downstream. If Rita starts from a certain location in the river, and returns downstream to the same location, taking a total of 100 minutes, then the total distance, in km, Rita will cover is

Suppose a,b,c are three distinct natural numbers, such that $$3ac=8(a+b)$$. Then, the smallest possible value of $$3a+2b+c$$ is

Let $$f(x)=\frac{x}{(2x-1)}$$ and $$g(x)=\frac{x}{(x-1)}$$. Then the domain of the funtion $$h(x)=f(g(x))+g(f(x))$$ is all real numbers except

A loan of Rs 1000 is fully repaid by two installments of Rs 530 and Rs 594, paid at the end of first and second year, respectively. If the interest is compounded annually, then the rate of interest, in percentage, is

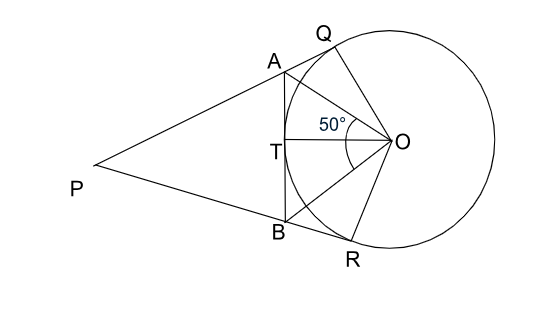
Two tangents drawn from a point p and a circle with center O at point Q and R. Point A and B lie on PQ and PR, repectively, Such that AB is also a tangent to the same circle. Ir $$\angle A0B=50^{0}$$, then $$\angle APB$$, in degrees equals

The number of divisors of $$(2^{6}\times 3^{5}\times 5^{3}\times 7^{2})$$, which are of the form $$(3r+1)$$, where r is a non-negative integer, is