Two tangents drawn from a point P and a circle with center O at point Q and R. Point A and B lie on PQ and PR, repectively, such that AB is also a tangent to the same circle. If $$\angle AOB=50^{0}$$, then $$\angle APB$$, in degrees equals

We can draw the following diagram as per the given question :

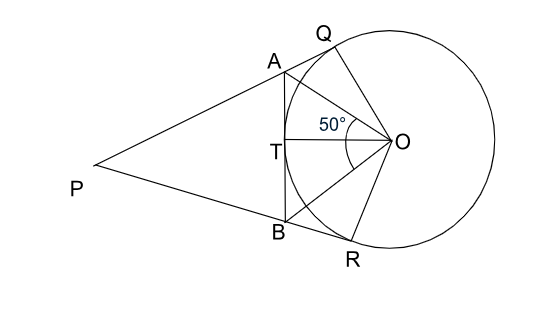
Now, taking $$\triangle AOT$$ and $$\triangle AOQ$$

AO is the common side

AT=AQ (Tangents drawn from an external point are equal in length)

OT=OQ (radius of circle)

So, by S.S.S., $$\triangle\ AOT$$ is congruent to $$\triangle\ AOQ$$

So, by C.P.C.T., $$\angle\ AOT=\angle\ AOQ$$

Similarly, for $$\triangle\ BOT\ $$ and $$\triangle\ BOR\ $$, we can do the same thing,

So, we can say $$\triangle\ BOT$$ and $$\triangle\ BOR$$ will also be congruent

Now, $$\angle\ QOR=\angle\ AOQ+\angle\ AOB+\angle\ ROB=\angle\ AOT+\angle\ AOB+\angle\ BOT=2\angle\ AOB=2\times\ 50^{\circ\ }=100^{\circ\ }$$

Now, in quadrilateral OQPR,

$$\angle\ OQP=\angle\ ORP=90^{\circ\ }$$ (Tangents drawn to a point is perpendicular to the radius drawn at the same point)

Now, sum of angles of a quadrilateral is $$360^{\circ\ }$$

So, $$\angle\ APB+\angle\ QOR=360^{\circ\ }-\left(90^{\circ\ }+90^{\circ\ }\right)=180^{\circ\ }$$

So, $$\angle\ APB=180^{\circ\ }-100^{\circ\ }=80^{\circ\ }$$