Sign in
Please select an account to continue using cracku.in
↓ →
The number of divisors of $$(2^{6}\times 3^{5}\times 5^{3}\times 7^{2})$$, which are of the form $$(3r+1)$$, where r is a non-negative integer, is
The divisors of the given number will have the form $$2^a*3^b*5^c*7^d$$ with $$0\le a\le6,\ 0\le b\le5,\ 0\le c\le3,\ 0\le d\le2$$
Because the divisors should be in the form 3r+1, it cannot be divisible by 3, so (b=0).
Reduce modulo 3: $$2 \text{mod} 3 = 2, 5 \text{mod} 3 = 2, 7 \text{mod} 3 = 1$$
Hence, $$2^a5^c7^d\equiv 2^{a+c}\cdot1^d \equiv 2^{a+c}\pmod3$$
2^k will be in the form 3r+1 only when K is even. So, we need a+c to be even
$$a\in{0,\dots,6}$$ has 4 even, 3 odd values
$$c\in{0,\dots,3}$$ has 2 even, 2 odd
Number of (a,c) with (a+c) even is $$4\cdot2 + 3\cdot2 = 8+6=14$$
For each such pair, there are 3 choices for d = 0,1,2. Thus, total divisors in the form (3r+1) equals $$14\times3=42$$.
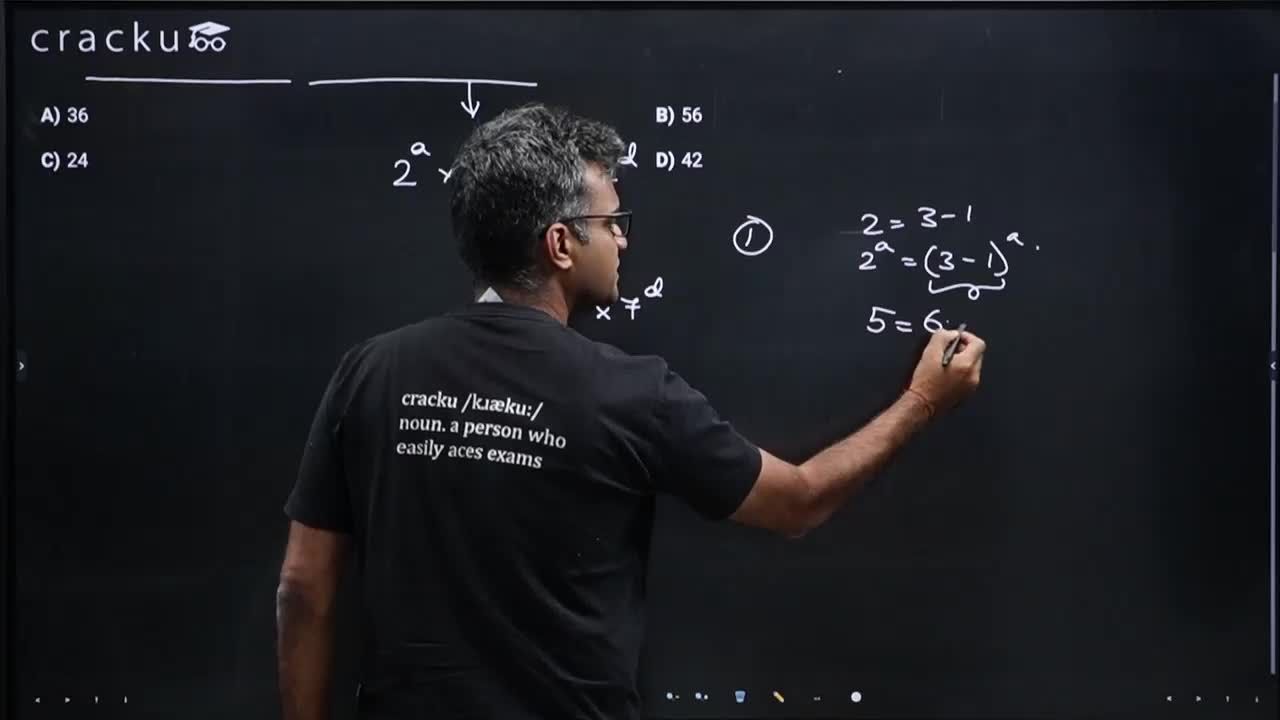
Click on the Email ☝️ to Watch the Video Solution
Create a FREE account and get:
Educational materials for CAT preparation