Let ABCDEF be a regular hexagon and P and Q be the midpoints of AB and CD, respectively. Then, the ratio of the areas of trapezium PBCQ and hexagon ABCDEF is

Let the side of the hexagon be a. 

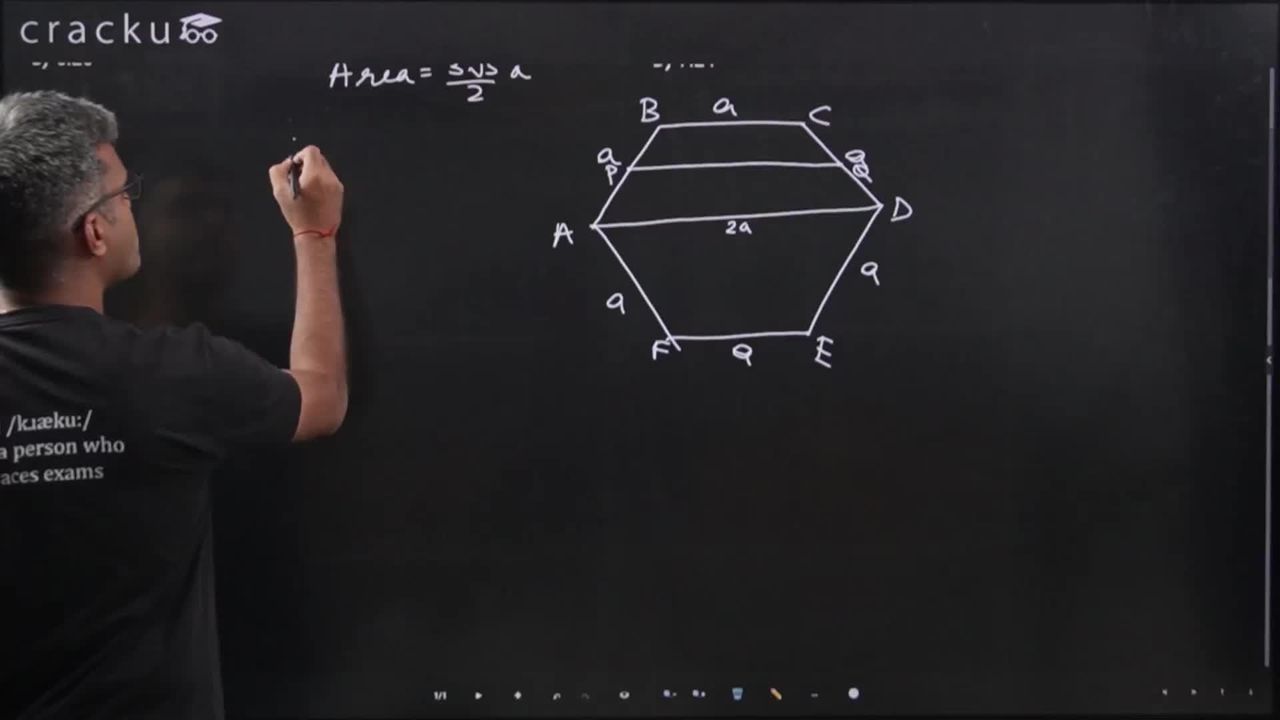
The area of the whole hexagon is going to be $$\frac{3\sqrt{3}a^2}{2}$$

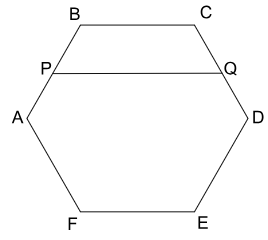
We know that the longest diagonal of a hexagon is 2 times the side of the hexagon.

PQ = $$\frac{\left(BC+AD\right)}{2}= \frac{\left(a+2a\right)}{2} =1.5a$$

The area of the trapezium =  Average of parllel sides * Height = $$\frac{\left(BC+PQ\right)}{2}\cdot h=\frac{5}{4}a\cdot h$$

The distance between BC and AD will be $$\sqrt{3}a$$, that is, the length of diagonal BF.

The distance between BC and AD will be $$\frac{\sqrt{3}a}{2}$$ 

And the height of the trapezium BCQP will be  $$\frac{\sqrt{3}a}{4}$$

Area of trapezium = $$\frac{5}{4}a\cdot \frac{\sqrt{3}a}{4}$$ = $$\frac{5\sqrt{3}a^2}{16}$$ 

Area of hexagon ABCDEF = $$\frac{3\sqrt{3}}{2}a^2$$

We have to find the ratio  = $$\frac{5\sqrt{3}a^2}{16}$$ : $$\frac{3\sqrt{3}}{2}a^2$$ = 5:24