Sign in
Please select an account to continue using cracku.in
↓ →
If m and n are integers such that $$(m+2n)(2m+n)=27$$, then the maximum possible value of $$2m-3n$$ is
Correct Answer: 17
Sure! We can solve it without explicitly introducing new variables for substitution.
We are given $$(m+2n)(2m+n) = 27$$ and we want to maximize $$2m-3n$$
Because m and n are integers, both (m+2n) and (2m+n) are going to be integers.
Factor pairs of 27 (including negatives) are: $$(1,27),(3,9),(9,3),(27,1),(-1,-27),(-3,-9),(-9,-3),(-27,-1)$$
For each factor pair (a,b), take $$a=m+2n$$, $$b=2m+n$$ and solve for integers (m,n).
If we notice $$a+b=\left(m+2n\right)+\left(2m+n\right)=3\left(m+n\right)$$
So, basically the sum of the two numbers has to be a multiple of $$3$$.
So, the ordered pairs we will consider are $$\left(3,9\right),\left(9,3\right),\left(-3,-9\right),\left(-9,-3\right)$$
For $$(a,b)=(9,3)$$:
$$ m+2n=9,\quad 2m+n=3 $$
Upon solving, we get $$n=5$$ and $$m=-1$$
For $$(a,b)=(3,9)$$:
$$ m+2n=3,\quad 2m+n=9 $$
Upon solving, we get $$n=-1$$ and $$m=5$$
Then $$2m-3n=2\cdot5-3(-1)=10+3=13$$
For negative factor pairs, we similarly get integer solutions $$(-5,1)$$ and $$(1,-5)$$, giving $$2m-3n=-13 \text{and} 17$$, respectively.
Thus, the maximum value of $$(2m-3n)$$ among all solutions is 17
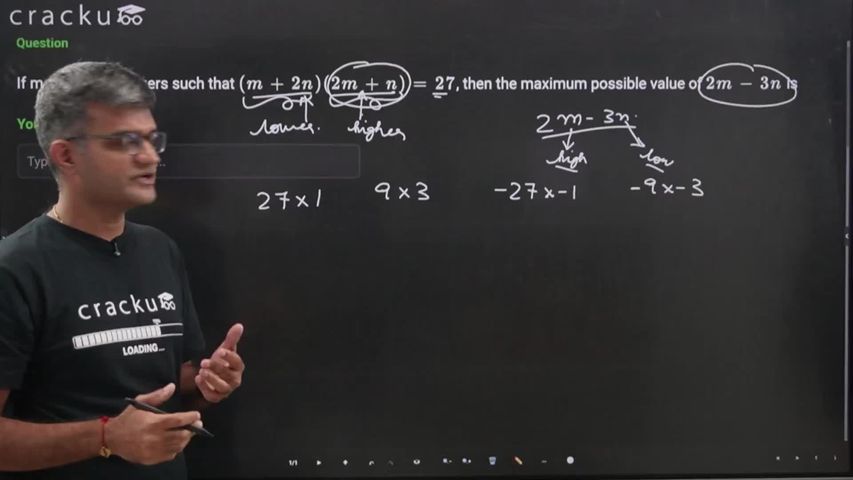
Click on the Email ☝️ to Watch the Video Solution
Create a FREE account and get:
Educational materials for CAT preparation