CAT 2025 Slot 2 Question Paper

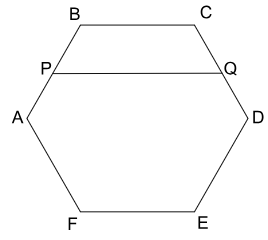
Let ABCDEF be a regular hexagon and P and Q be the midpoints of AB and CD, respectively. Then, the ratio of the areas of trapezium PBCQ and hexagon ABCDEF is

If a,b,c and d are integers such that their sum is 46, then the minimum possible value of $$(a-b)^{2}+(a-c)^{2}+(a-d)^{2}$$ is

The ratio of expenditures of Lakshmi and Meenakshi is 2 : 3, and the ratio of income of Lakshmi to expenditure of Meenakshi is 6 : 7. If excess of income over expenditure is saved by Lakshmi and Meenakshi, and the ratio of their savings is 4 : 9, then the ratio of their incomes is

Let $$a_{n}$$ be the $$n^{th}$$term of a decreasing infinite geometric progression. If $$a_{1}+a_{2}+a_{3}=52$$ and $$a_{1}a_{2}+a_{2}a_{3}+a_{3}a_{1}=624$$, then the sum of this geometricc progression is

A mixture of coffee and cocoa, 16% of which is coffee, costs Rs 240 per kg. Another mixture of coffee and cocoa, of which 36% is coffee, costs Rs 320 per kg. If a new mixture of coffee and cocoa costs Rs 376 per kg, then the quantity, in kg, of coffee in 10 kg of this new mixture is

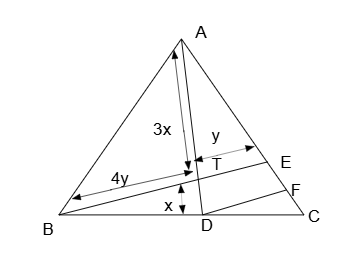
In $$\triangle ABC$$, points D and E are on the sides BC and AC, respectively. BE and AD intrested at point T such that AD:AT=4:3, and BE:BT=5:4. Point F lies on AC such that DF is parallel to BE. Then, BD:CD is

Ankita is twice as efficient as Bipin, while Bipin is twice as efficient as Chandan. All three of them start together on a job, and Bipin leaves the job after 20 days. If the job got completed in 60 days, the number of days needed by Chandan to complete the job alone, is

A certain amount of money was divided among Pinu, Meena, Rinu and Seema. Pinu received 20% of the total amount and Meena received 40% of the
remaining amount. If Seema received 20% less than Pinu, the ratio of the amounts received by Pinu and Rinu is