In $$\triangle ABC$$, points D and E are on the sides BC and AC, respectively. BE and AD intersect at point T such that AD:AT=4:3, and BE:BT=5:4. Point F lies on AC such that DF is parallel to BE. Then, BD:CD is

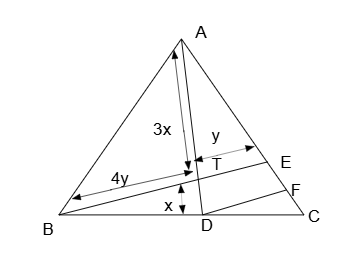
In the question, it is given $$AD:AT=4:3$$

So,$$TD:AT=1:3$$

Let, $$TD=x,\ AT=3x$$

Also, $$BE:BT=5:4$$

So, $$BT:TE=4:1$$

Let, $$BT=4y,\ TE=y$$

Given, DF is parallel to BE

So, DF is parallel to TE

So, $$\triangle\ ATE~\triangle\ ADF$$ (by A.A., as $$\angle\ ATE=\angle\ ADF$$ and $$\angle\ AET=\angle\ AFD$$)

So, $$\dfrac{AT}{AD}=\dfrac{TE}{DF}$$

So, $$\dfrac{3x}{x+3x}=\dfrac{y}{DF}$$

So, $$DF=\dfrac{4y}{3}$$

Also, since DF is parallel to BE,

So, $$\triangle\ CFD~\triangle\ CBE$$ (by A.A., as $$\angle\ CFD=\angle\ CEB$$ and $$\angle\ CDF=\angle\ CBE$$)

So, $$\dfrac{CD}{BC}=\dfrac{DF}{BE}$$

So, $$\dfrac{CD}{BC}=\dfrac{\dfrac{4y}{3}}{5y}=\dfrac{4y}{15y}=\dfrac{4}{15}$$

So, $$\dfrac{CD}{BD}=\dfrac{4}{11}$$

So, $$BD:CD=11:4$$