CAT 2003 Question Paper (Leaked)
For the following questions answer them individually
CAT 2003 (Leaked) - Question 81
How many three digit positive integers, with digits x, y and z in the hundred's, ten's and unit's place respectively, exist such that x < y, z < y and x $$\neq$$ 0 ?
CAT 2003 (Leaked) - Question 82
A vertical tower OP stands at the center O of a square ABCD. Let h and b denote the length OP and AB respectively. Suppose $$\angle{APB}$$ = 60° then the relationship between h and b can be expressed as
CAT 2003 (Leaked) - Question 83
In the triangle ABC, AB = 6, BC = 8 and AC = 10. A perpendicular dropped from B, meets the side AC at D. A circle of radius BD (with center B) is drawn. If the circle cuts AB and BC at P and Q respectively, the AP:QC is equal to
CAT 2003 (Leaked) - Question 84
In the diagram given below, $$\angle{ABD}$$ = $$\angle{CDB}$$ = $$\angle{PQD}$$ = 90° . If AB:CD = 3:1, the ratio of CD: PQ is

CAT 2003 (Leaked) - Question 85
There are 8436 steel balls, each with a radius of 1 centimeter, stacked in a pile, with 1 ball on top, 3 balls in the second layer, 6 in the third layer, 10 in the fourth, and so on. The number of horizontal layers in the pile is
CAT 2003 (Leaked) - Question 86
If the product of n positive real numbers is unity, then their sum is necessarily
CAT 2003 (Leaked) - Question 87
If $$log_3 2, log_3 (2^x - 5), log_3 (2^x - 7/2)$$ are in arithmetic progression, then the value of x is equal to
CAT 2003 (Leaked) - Question 88
In the figure below, AB is the chord of a circle with center O. AB is extended to C such that BC = OB. The straight line CO is produced to meet the circle at D. If $$\angle{ACD}$$ = y degrees and $$\angle{AOD}$$ = x degrees such that x = ky, then the value of k is
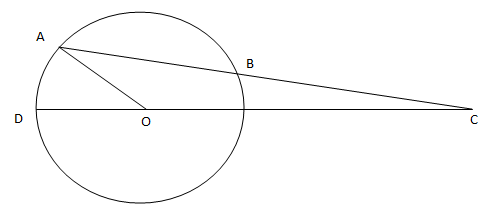
CAT 2003 (Leaked) - Question 89
In the figure below, the rectangle at the corner measures 10 cm × 20 cm. The corner A of the rectangle is also a point on the circumference of the circle. What is the radius of the circle in cm?

CAT 2003 (Leaked) - Question 90
Given that $$-1 \leq v \leq 1, -2 \leq u \leq -0.5$$ and $$-2 \leq z \leq -0.5$$ and $$w = vz /u$$ , then which of the following is necessarily true?
Two Factor Authentication
Incase of any issue contact support@cracku.in








