CAT 2003 Question Paper (Leaked)
For the following questions answer them individually
CAT 2003 (Leaked) - Question 71
Is $$(1/a^2 + 1/a^4 + 1/a^6 +...) > (1/a + 1/a^3 + 1/a^5 +...)$$?
A. $$0< a \leq 1$$
B. One of the roots of the equation $$4x^2-4x+1 = 0$$ is a
CAT 2003 (Leaked) - Question 72
D, E, F are the mid points of the sides AB, BC and CA of triangle ABC respectively. What is the area of DEF in square centimeters?
A. AD = 1 cm, DF = 1 cm and perimeter of DEF = 3 cm
B. Perimeter of ABC = 6 cm, AB = 2 cm, and AC = 2 cm.
CAT 2003 (Leaked) - Question 73
At the end of year 1998, Shepard bought nine dozen goats. Henceforth, every year he added p% of the goats at the beginning of the year and sold q% of the goats at the end of the year where p > 0 and q > 0. If Shepard had nine dozen goats at the end of year 2002, after making the sales for that year, which of the following is true?
CAT 2003 (Leaked) - Question 74
Each side of a given polygon is parallel to either the X or the Y axis. A corner of such a polygon is said to be convex if the internal angle is 90° or concave if the internal angle is 270°. If the number of convex corners in such a polygon is 25, the number of concave corners must be
CAT 2003 (Leaked) - Question 75
The 288th term of the series a,b,b,c,c,c,d,d,d,d,e,e,e,e,e,f,f,f,f,f,f… is
CAT 2003 (Leaked) - Question 76
Let p and q be the roots of the quadratic equation $$x^2 - (\alpha - 2) x - \alpha -1= 0$$ . What is the minimum possible value of $$p^2 + q^2$$?
CAT 2003 (Leaked) - Question 77
There are two concentric circles such that the area of the outer circle is four times the area of the inner circle. Let A, B and C be three distinct points on the perimeter of the outer circle such that AB and AC are tangents to the inner circle. If the area of the outer circle is 12 square centimeters then the area (in square centimeters) of the triangle ABC would be
CAT 2003 (Leaked) - Question 78
Let a, b, c, d be four integers such that a+b+c+d = 4m+1 where m is a positive integer. Given m, which one of the following is necessarily true?
CAT 2003 (Leaked) - Question 79
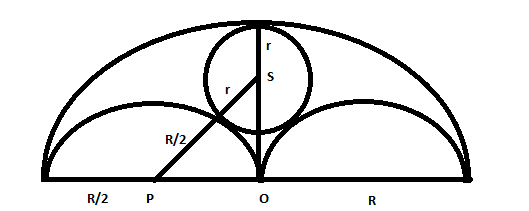
Three horses are grazing within a semi-circular field. In the diagram given below, AB is the diameter of the semi-circular field with center at O. Horses are tied up at P, R and S such that PO and RO are the radii of semi-circles with centers at P and R respectively, and S is the center of the circle touching the two semi-circles with diameters AO and OB. The horses tied at P and R can graze within the respective semi-circles and the horse tied at S can graze within the circle centred at S. The percentage of the area of the semi-circle with diameter AB that cannot be grazed by the horses is nearest to

CAT 2003 (Leaked) - Question 80
In the figure below, ABCDEF is a regular hexagon and $$\angle{AOF}$$ = 90° . FO is parallel to ED. What is the ratio of the area of the triangle AOF to that of the hexagon ABCDEF?

Two Factor Authentication
Incase of any issue contact support@cracku.in