CAT 2001 Question Paper
Directions for the following two questions: Answer the questions based on the following information.
The batting average (BA) of a Test batsman is computed from runs scored and innings played — completed innings and incomplete innings (not out) in the following manner:
$$r_1 =$$ Number of runs scored in completed innings
$$n_1 =$$ Number of completed innings
$$r_2 =$$ Number of runs scored in incomplete innings
$$n_2 =$$ Number of incomplete innings
$$BA=\frac{r_1+r_2}{n_1}$$
To better assess a batsman’s accomplishments, the ICC is considering two other measures $$MBA_1$$ and $$MBA_2$$ defined as follows:
$$MBA_1 = \frac{r_1}{n_1} + \frac{n_2}{n_1}*max[0,(\frac{r_2}{n_2}-\frac{r_1}{n_1})]$$
$$MBA_2 = \frac{r_1 + r_2}{n_1 + n_2}$$
CAT 2001 - Question 2
An experienced cricketer with no incomplete innings has BA of 50. The next time he bats, the innings is incomplete and he scores 45 runs. It can be inferred that
Directions for the following two questions: Answer the questions based on the following information.
The petrol consumption rate of a new model car ‘Palto’ depends on its speed and may be described by the graph below.
The axis represents the speed and the Y axis represents the Fuel Consumption (Liters per hour)

CAT 2001 - Question 3
Manasa makes a 200 km trip from Mumbai to Pune at a steady speed of 60 km/hr. What is the volume of petrol consumed for the journey?
[CAT 2001]
CAT 2001 - Question 4
Manasa would like to minimize the fuel consumption for the trip by driving at the appropriate speed. How should she change the speed?
[CAT 2001]
For the following questions answer them individually
CAT 2001 - Question 5
A student took five papers in an examination, where the full marks were the same for each paper. His marks in these papers were in the proportion of 6 : 7 : 8 : 9 : 10. In all papers together, the candidate obtained 60% of the total marks. Then the number of papers in which he got more than 50% marks is
CAT 2001 - Question 6
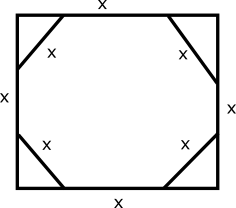
A square, whose side is 2 m, has its corners cut away so as to form an octagon with all sides equal. Then the length of each side of the octagon, in metres, is
CAT 2001 - Question 7
Let x, y and z be distinct integers. x and y are odd and positive, and z is even and positive. Which one of the following statements cannot be true?
CAT 2001 - Question 8
If x > 5 and y < -1, then which of the following statements is true?
CAT 2001 - Question 9
A red light flashes three times per minute and a green light flashes five times in 2 min at regular intervals. If both lights start flashing at the same time, how many times do they flash together in each hour?
CAT 2001 - Question 10
Of 128 boxes of oranges, each box contains at least 120 and at most 144 oranges. X is the maximum number of boxes containing the same number of oranges. What is the minimum value of X?