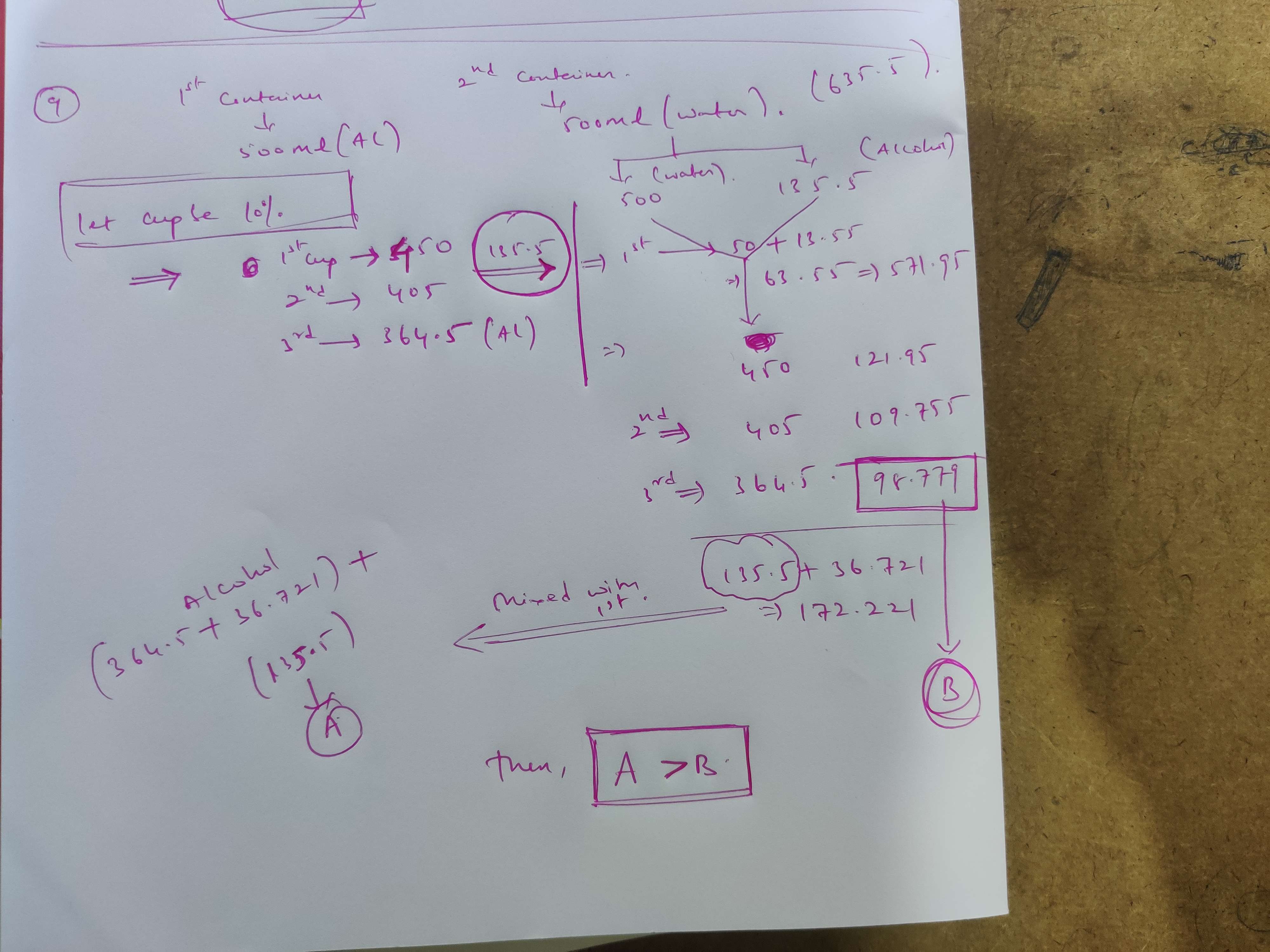
There are two containers: the first contains 500 ml of alcohol, while the second contains 500 ml of water. Three cups of alcohol from the first container is taken out and is mixed well in the second container. Then three cups of this mixture is taken out and is mixed in the first container. Let A denote the proportion of water in the first container and B denote the proportion of alcohol in the second container. Then,
Let the volume of the cup be V.
Hence, after removing three cups of alcohol from the first container,
Volume of alcohol in the first container is 500-3V
Volume of water in the second container is 500 and volume of alcohol in the second container is 3V.
So, in each cup, the amount of water contained is $$\frac{500}{500+3V}*V$$
Hence, after adding back 3 cups of the mixture, amount of water in the first container is $$0+\frac{1500V}{500+3V} $$
Amount of alcohol contained in the second container is $$3V - \frac{9V^2}{500+3V} = \frac{1500V}{500+3V}$$
So, the required proportion of water in the first container and alcohol in the second container are equal.
Video Solution

Your Doubts
Create a FREE account and get:
- All Quant CAT complete Formulas and shortcuts PDF
- 38+ CAT previous year papers with video solutions PDF
- 5000+ Topic-wise Previous year CAT Solved Questions for Free