Please enter the following details
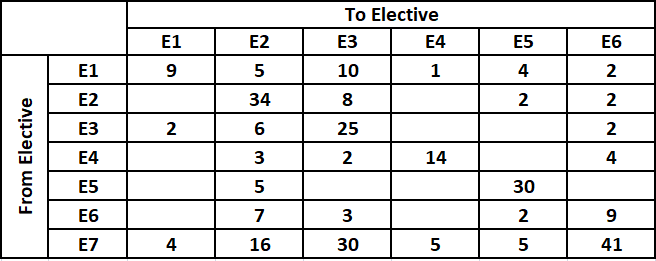
There were seven elective courses - E1 to E7 - running in a specific term in a college. Each of the 300 students enrolled had chosen just one elective from among these seven. However, before the start of the term, E7 was withdrawn as the instructor concerned had left the college. The students who had opted for E7 were allowed to join any of the remaining electives. Also, the students who had chosen other electives were given one chance to change their choice. The table below captures the movement of the students from one elective to another during this process. Movement from one elective to the same elective simply means no movement. Some numbers in the table got accidentally erased; however, it is known that these were either 0 or 1.
Further, the following are known:
1. Before the change process there were 6 more students in E1 than in E4, but after the reshuffle, the number of students in E4 was 3 more than that in E1.
2. The number of students in E2 increased by 30 after the change process.
3. Before the change process, E4 had 2 more students than E6, while E2 had 10 more students than E3.
Later, the college imposed a condition that if after the change of electives, the enrollment in any elective (other than E7) dropped to less than 20 students, all the students who had left that course will be required to re-enroll for that elective.
Which of the following is a correct sequence of electives in decreasing order of their final enrollments?
From the table we can say that number of students who opted for E2 after reshuffle = 5 + 34 + 6 + 3 + 5 + 7 + 16 = 76.
It is given us that the number of students in E2 increased by 30 after the change process. Hence, we can say that the number of students who were enrolled in E2 before reshuffle = 76 - 30 = 46.
It is given that before the change process there were 10 more students in E2 than in E3. Therefore, the number of students who were enrolled in E3 before reshuffle = 46 - 10 = 36.
Number of students who moved from E1 to all other electives are known. Therefore, the number of students who were enrolled in E1 before reshuffle = 9 + 5 + 10 + 1 + 4 + 2 = 31.
It is given that before the change process there were 6 more students in E1 than in E4. Therefore, the number of students who were enrolled in E4 before reshuffle = 31 - 6 = 25.
Also, it is given that E4 had 2 more students than E6 before reshuffle. Therefore, the number of students who were enrolled in E6 before reshuffle = 25 - 2 = 23.
All the students from E7 moved to one of electives among E1 to E6. Therefore, the number of students who were enrolled in E7 before reshuffle = 4 + 16 + 30 + 5 + 5 + 41 = 101.
Except E5 we know the number of students who were enrolled in all electives. We also know that there were total 300 students who opted for exactly 1 elective.
Hence, the the number of students who were enrolled in E7 before reshuffle = 300 - (46+36+31+25+23+101) = 38.
For each elective, the number of students who were enrolled before reshuffle will be same as sum of the number of students who moved from that elective to another elective including no movement cases.
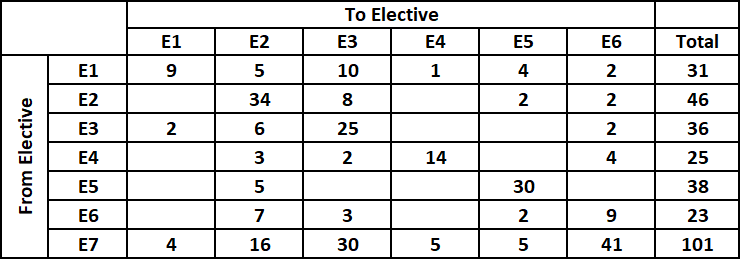
For elective E2,
Number of students who moved to E1 + 34 + 8 + Number of students who moved to E4 + 2 + 2 = 46
i.e. Number of students who moved from to E1 = Number of students who moved from to E4 = 0
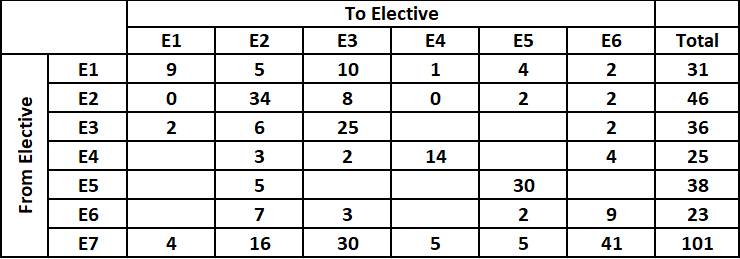
For elective E4,
Number of students who moved to E1 + 3 + 2 + 14 + Number of students who moved to E5 + 4 = 25
i.e. Number of students who moved from to E1 = Number of students who moved from to E5 = 1 {As the remaining blanks can be filled by either 0 or 1}
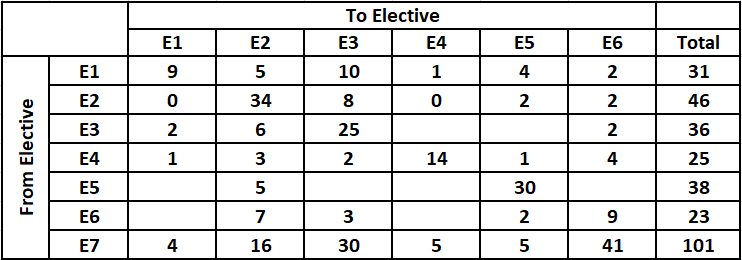
For elective E6,
Number of students who moved to E1 + 7 + 3 + Number of students who moved to E4 + 2 + 9 = 23
i.e. Number of students who moved from to E1 = Number of students who moved from to E4 = 1 {As the remaining blanks can be filled by either 0 or 1}
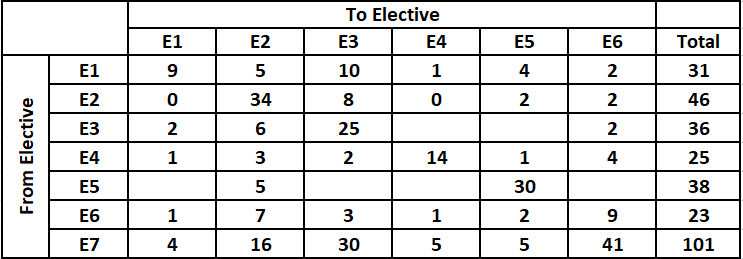
It is given that after the reshuffle, the number of students in E4 was 3 more than that in E1. As of now the number of students enrolled in E4 after reshuffle = 1 + 0 + E3 to E4 + 14 + E5 to E4 + 1 + 5 = 21 + {E3 to E4} + {E5 to E4}
Also, the number of students enrolled in E1 after reshuffle = 9 + 0 + 2 + 1 + E5 to E1 + 1 + 4 = 17 + E5 to E1.
Hence, it is possible only when E5 to E1 = 1 and E3 to E4 = E5 to E4 = 0.
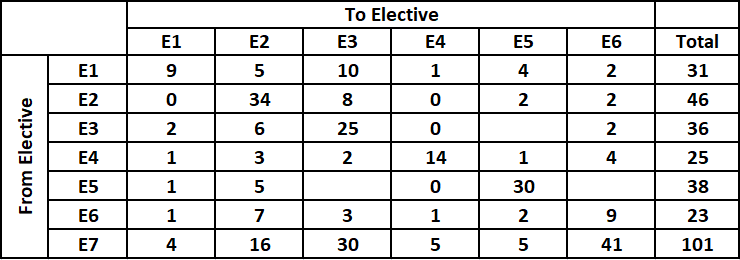
Remaining blank places can be filled easily as we know the total sum of each row.
Therefore, the number of students who moved from E3 to E5 = the number of students who moved from E5 to E3 = the number of students who moved from E5 to E6 = 1.
We can see from the table that number of students enrolled in E1 dropped to 18. Hence, all the students who moved from E1 to any other elective will have to re-enroll in E1.
We can see that the number of students who enrolled for E1 prior to reshuffle = 31. Out of these 31 students, 9 students didn't move to any other elective whereas remaining 22 students moved to other electives. Hence, all these 22 students have to re-enroll in E1.
Therefore, the total number of students in E1 post re-enrollment = 18 + 22 = 40 which is shown in the table.
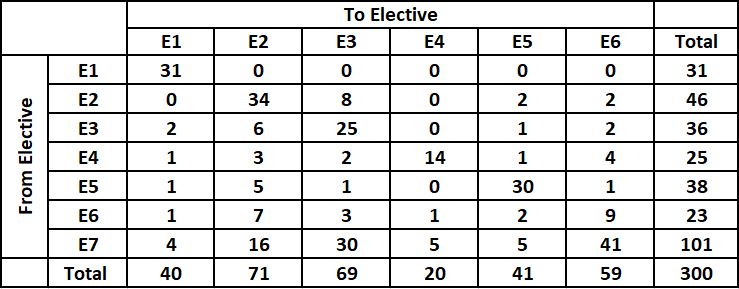
Therefore, the sequence of electives in decreasing order of their final enrollments = E2, E3, E6, E5, E1, E4.
Hence, option A is the correct answer.
Video Solution
Create a FREE account and get:
- All Quant CAT complete Formulas and shortcuts PDF
- 35+ CAT previous year papers with video solutions PDF
- 5000+ Topic-wise Previous year CAT Solved Questions for Free
