Top 100 CAT 2025 Quant Questions PDF
Cracku’s Top 100 CAT 2025 Quant Questions PDF with Video Solutions is a complete guide to improve your CAT Quant preparation. It includes important topics like Arithmetic, Algebra, Geometry, and Modern Math to help you build strong basics and improve your problem-solving skills.
Each question comes with a clear video explanation, making it easy to learn shortcuts, tricks, and smart methods. Whether you’re aiming for a 99+ percentile or just want to strengthen your fundamentals, these 100 questions will get you ready for all levels of CAT 2025 quant questions.
Why Practice with Cracku’s Top 100 Quant Questions for CAT 2025?
The CAT 2025 Quant section needs both speed and accuracy. Practicing well-made questions with step-by-step video solutions helps you:
-
Understand key Quant concepts easily
-
Improve your speed and accuracy under time pressure
-
Learn smart solving methods from expert explanations
With the CAT 2025 Quant PDF and Video Solutions, you can revise quickly, clear your doubts, and build the confidence needed to solve even the toughest Quant questions in the exam.
Question 1
A container was half-filled with liquid A having p and q in the ratio 3:5. Liquid p evaporates at the rate of 2 liters per minute and Liquid q evaporates at the rate of 3 liters per minute for half an hour. After half an hour, the same container was totally filled with liquid B having q and p in the ratio 2:3. If the ratio p:q is 11:9 after the addition of liquid B, then what is the capacity of the container (in liter)?
correct answer:- 480
Question 2
The mean score of ten batsmen of Hyderabad cricket team in a match is 60. If the top five scores of the batsmen are removed while calculating the average, the average falls by five. If the top six scores are distinct integers, what is the maximum possible score of any batsmen?
correct answer:- 3
Question 3
From a can of 50 litres of milk, 10 litres are withdrawn and replaced with water. Again, 8 litres are removed and replaced with water. Similarly, the quantity of mixture withdrawn and replaced by water is decreased by 2 litres and repeated until the step when 2 litres of the mixture is removed and replaced with water. What will be the quantity of milk left in the final mixture?
correct answer:- 1
Question 4
Ravi was having a party at his house where he invited some of his friends. There were two types of juices which were available at the party, i.e apple juice and orange juice. Each member drank some apple juice and some orange juice. Although there was variation in the amount of apple juice and orange juice consumed by different members, it is known that the total juice consumed by each person was 1300 ml. Ravi drank one fifth of the total apple juice which was consumed at the party and he also consumed one seventh of the total orange juice which was consumed at the party. What was the ratio of orange juice and apple juice consumed by Ravi at the party? (Apple or orange juice consumed by any person is an integral multiple of '1' ml)
correct answer:- 3
Question 5
In a certain infinite geometric progression, the sum of any three consecutive terms equals 26 times the sum of all the terms that follow them. What is the ratio of any term of the progression to the sum of all the terms that follow it?
correct answer:- 3
Question 6
A contains 100 litres of pure milk while B contains 200 litres of water. 40 litres is removed from A and inserted into B and 40 litres of the resulting solution is removed from B and inserted into A. This process is repeated indefinitely. What is final% of milk in A?
correct answer:- 2
Question 7
Four unique even numbers are arranged in ascending order and the first two are decreased by 50%, while the last two are increased by 50%. If the original sum of the 4 numbers was 162, the new sum can be?
correct answer:- 3
Question 8
A shopkeeper buys 3 varieties of rice for Rs 20, Rs 30 and Rs 40 per kg respectively. He now mixes the 3 varieties in the ratio 5:6:7 by weight and sells the mixture at a profit of 10%. What price per kg does he sell the mixture for?
correct answer:- 3
Question 9
A contractor agreed to construct a 6 km road in 200 days. He employed 140 persons for the work. After 60 days, he realized that only 1.5 km road has been completed. How many additional people would he need to employ in order to finish the work exactly on time?
correct answer:- 40
Question 10
A, B, C, D are standing in clockwise direction at the corners of a square of side 's'. They are start running clockwise along the sides of the square with speeds in the ratio 1:2:3:4 respectively. How much distance does A run by the time they all meet for the third time?
correct answer:- 1
Question 11
Five pipes A, B, C, D, and E can fill a tank in 60 minutes, 20 minutes, 30 minutes, 8 minutes, 32 minutes respectively. Out of these five pipes, two have now been converted into emptying pipes such that their efficiency remains the same. When only one of filling pipes and one of the emptying pipes operate, the tank can be filled in 60 minutes. Another combination of one filling and one emptying pipes empties the tank in $$\frac{8}{45}^{th}$$ of the time taken by the previous combination to fill the tank. Which pipes are converted into emptying pipes?
correct answer:- 4
Question 12
A train travelled at one-thirds of its usual speed, and hence reached the destination 30 minutes after the scheduled time. On its return journey, the train initially travelled at its usual speed for 5 minutes but then stopped for 4 minutes for an emergency. The percentage by which the train must now increase its usual speed so as to reach the destination at the scheduled time, is nearest to
correct answer:- 3
Question 13
A bus starts from A and moves towards B at 25 km/hr. At the same time, another bus starts from B and moves towards A at 35 km/hr. Once they reach their destination, they turn back and move towards the point from where it started and go on till infinite time. So, the bus that starts from A, moves to B, turns back and moves back to A, then again to B, then again back to A and so on.
Whenever they meet, while going in opposite directions, the drivers wave to each other. What is the distance between the points where they wave for the first time and where they wave for the 10th time? A and B are 18 km apart.
correct answer:- 1
Question 14
Mr. Vinay walks up on a moving up escalator to save time. He takes 100 steps while going up. On one particular day, due to a power failure for 20 seconds, he took 18 seconds more than his usual time to reach the top of the escalator. How many steps are there on the escalator?
correct answer:- 4
Question 15
Two boats A and B are travelling in opposite directions in still water. The ratio of the distances covered by them in the same time is 3:1. If they travel in opposite directions in a stream, the distance covered by A and B (in the same time) is 1:3 respectively. What is the ratio of the speed of A and speed of the water?
correct answer:- 2
Question 16
Aman and Bala started running from the same point around a hexagonal track. They started running in the same direction with their speed in the ratio a:b. If they meet each other only at the corners of the hexagon, not necessarily all corners, which of the following cannot be the value of the ratio a:b?
correct answer:- 4
Question 17
5 boys and 3 men complete a work in 15 days. 5 men start working and after 6 days, 10 boys join and the work is completed in 4 more days. the efficiency of 1 man is equal to that of
correct answer:- 3
Question 18
On a straight road, there are two points P and Q. Virat and Rohit are standing at points P and Q are respectively. They start running towards each other at constant speeds. As soon as they reach the opposite point, they immediately turn back and run towards their respective starting point. The same process continues till each one of them has completed 10 trips (1 trip is going to the opposite point and returning back). Virat and Rohit meet for the first time 540 m away from P and their second meeting takes place 600 m away from Q. Find the distance (in m) of their third meeting point from Q. (It is known that the two persons never cross each other while travelling in the same direction)
correct answer:- 360
Question 19
Ten men can complete a piece of work in 8 days while fifteen women take 6 days to complete the work. If 9 women and x men can complete the work in 8 days. What is the value of x?
correct answer:- 3
Question 20
Vimla starts for office every day at 9 am and reaches exactly on time if she drives at her usual speed of 40 km/hr. She is late by 6 minutes if she drives at 35 km/hr. One day, she covers two-thirds of her distance to office in one-thirds of her usual total time to reach office, and then stops for 8 minutes. The speed, in km/hr, at which she should drive the remaining distance to reach office exactly on time is
correct answer:- 3
Question 21
Pipes A, B and C are fitted to a tank such that A is an inlet pipe, B and C are outlet pipes. Pipe A is at the bottom of the tank, Pipe B is situated at half the height of the tank while C is situated at one fourth the height of the tank from the bottom. All the pipes are opened simultaneously for an empty tank. The ratio of the outlet flow of pipes B & C is 1:5. The tank is full in a total of 16 hours and was half-filled in 6 hours. Which of the following is the ratio of the rate of flow of in pipe A to pipe B?
correct answer:- 1
Question 22
The cost price of two scooters is in the ratio of 3:4. Ajay made Rs. 1 lakh and Rs. 2 lakh profit on each of them respectively. Which of the following can't be the ratio of their selling price?
correct answer:- 3
Question 23
Raj invested ₹ 10000 in a fund. At the end of first year, he incurred a loss but his balance was more than ₹ 5000. This balance, when invested for another year, grew and the percentage of growth in the second year was five times the percentage of loss in the first year. If the gain of Raj from the initial investment over the two year period is 35%, then the percentage of loss in the first year is
correct answer:- 4
Question 24
A shopkeeper obtains a profit of 25% on an item by selling it at marked price. If the cost price and the marked price of the product increases by 10%, what discount should the shopkeeper give on the marked price, so that the overall profit comes down to 20% ?
correct answer:- 3
Question 25
A particular mobile phone was sold to a customer at 5% loss. If he had sold it for 90 Rs more, the shopkeeper would have made a profit of 1%. . Find the initial cost price of the mobile phone.
correct answer:- 4
Question 26
A shopkeeper buys wheat at a wholesale price of Rs 85 per bag. He sells 40% of the bags at a price of Rs 60 each. At what price should he sell the remaining bags so that he makes an overall profit of 10%?
correct answer:- 1
Question 27
Ayra, Myra and Kiara invested in a business. Myra started investing Rs 6000 per month at the beginning of the year. After 4 months, Ayra started investing in business with Rs 6000 per month, and later, Kiara started investing with Rs 12000 per month. After a year, it is known that Myra received 50% of the profit. How many months after Ayra did Kiara invest?
correct answer:- 4
Question 28
A milkman has 20 litres milk. He replaces it with x litres of water once and sells it at the original cost price of the milk such that the profit percentage is 25. Assuming, water is free, the value of x is
correct answer:- 4
Question 29
Monika buys a Samsung’s 360 litre refrigerator from M/s Coldrush Agencies for ₹ 42,000. She makes a down payment of ₹ 12,000 and the remaining amount in 4 equal half yearly instalments. If M/s Coldrush Agencies charge an interest of 10% per annum, approximately what amount Monika has to pay every six month ?
correct answer:- 3
Question 30
A certain amount is given at compound interest and the amount increased by 27% between the 2nd year and 4th year. After how many years does the amount double itself?
correct answer:- 3
Question 31
Swarn a SME enterprise borrowed a sum of money from a nationalized bank at 10% simple interest per annum and the same amount at 8% simple interest per annum from a microfinance firm for the same period: It cleared the first loan 6 months before the scheduled date of repayment and repaid the second loan just at the end of the scheduled period: If in each case it had to pay Rs. 62100 as amount then how much money and for what time period did it borrow?
correct answer:- 3
Question 32
Bank A offers 6% interest rate per annum compounded half-yearly. Bank B and Bank C offer simple interest but the annual interest rate offered by Bank C is twice that of Bank B. Raju invests a certain amount in Bank B for a certain period and Rupa invests ₹ 10,000 in Bank C for twice that period. The interest that would accrue to Raju during that period is equal to the interest that would have accrued had he invested the same amount in Bank A for one year. The interest accrued, in INR, to Rupa is
correct answer:- 2
Question 33
The compound interest paid by a person in 8 years is 5 times the compound interest paid by him in 4 years, then find the approximate annual rate of the interest.
correct answer:- 3
Question 34
Veeru invested Rs 10000 at 5% simple annual interest, and exactly after two years, Joy invested Rs 8000 at 10% simple annual interest. How many years after Veeru’s investment, will their balances, i.e., principal plus accumulated interest, be equal?
correct answer:- 12
Question 35
A gentleman decided to treat a few children in the following manner. He gives half of his total stock of toffees and one extra to the first child, and then the half of the remaining stock along with one extra to the second and continues giving away in this fashion. His total stock exhausts after he takes care of 5 children. How many toffees were there in his stock initially?
correct answer:- 62
Question 36
If $$3x+2\mid y\mid+y=7$$ and $$x+\mid x \mid+3y=1$$ then $$x+2y$$ is:
correct answer:- 3
Question 37
If |x+y|+|x-y| = 8. Then the maximum value of $$x^2+y^2+3xy$$
correct answer:- 80
Question 38
A basket of 2 apples, 4 oranges and 6 mangoes costs the same as a basket of 1 apple, 4 oranges and 8 mangoes, or a basket of 8 oranges and 7 mangoes. Then the number of mangoes in a basket of mangoes that has the same cost as the other baskets is
correct answer:- 2
Question 39
4x-3y+2=0. If (a,b) is a solution of the equation, find the value of the expression $$-8^b\left(\dfrac{\left(492a-369b\right)}{16^a}\right)$$.
(Enter your answer as the nearest integer. Enter -1 if cannot be determined)
correct answer:- 984
Question 40
Let A, B and C be three positive integers such that the sum of A and the mean of B and C is 5. In addition, the sum of B and the mean of A and C is 7. Then the sum of A and B is
correct answer:- 3
Question 41
f(x) is a four-degree polynomial and the coefficient of $$\text{x}^4$$ is 1.
If f(1) = 5, f(2) = 10, f(3) = 15 and f(4) = 20 then, what is the value of f(5)?
correct answer:- 3
Question 42
If $$\log_9\left(x-1\right)\ =\ \log_3\left(x-3\right)$$, then the sum of all the possible solutions of x is
correct answer:- 5
Question 43
Consider the pair of equations: $$x^{2}-xy-x=22$$ and $$y^{2}-xy+y=34$$. If $$x>y$$, then $$x-y$$ equals
correct answer:- 4
Question 44
Suppose one of the roots of the equation $$ax^{2}-bx+c=0$$ is $$2+\sqrt{3}$$, Where a,b and c are rational numbers and $$a\neq0$$. If $$b=c^{3}$$ then $$\mid a\mid$$ equals.
correct answer:- 2
Question 45
If f(x) = $$x^2-4x+4$$, find out the sum of roots of the equation f(f(x)) = 9.
correct answer:- 3
Question 46
If a,b,c are roots of the equation $$x^3 - Px^2 + 108x -216 = 0$$ and $$a^3+b^3+c^3=648$$, find the value of P, if a,b and c are all positive?
correct answer:- 2
Question 47
The number of distinct pairs of integers (m,n), satisfying $$\mid1+mn\mid<\mid m+n\mid<5$$ is:
correct answer:- 12
Question 48
The solution set of $$\log_{\ \frac{\ 3}{4}}\left(\frac{x-4}{x-1}\right)\ >\ 0$$ is
correct answer:- 3
Question 49
The number of integers n that satisfy the inequalities $$\mid n - 60 \mid < \mid n - 100 \mid < \mid n - 20 \mid$$ is
correct answer:- 2
Question 50
For how many integers, $$x$$, is $$\log_2\log_3\left(\ \dfrac{\ x^2+2}{x+14}\right)$$ less than 0?
correct answer:- 2
Question 51
For real x, if $$x^2-5x+\frac{1}{x^2}-\frac{5}{x}-4\le0$$. Find the difference of the largest and smallest possible integral value of x.
correct answer:- 4
Question 52
Which of the following value of x does not satisfy the following inequality: (x+1)$$\log_{10}\left(3-x^2\right)$$ < 0
correct answer:- 4
Question 53
In a group of 10 students, the mean of the lowest 9 scores is 42 while the mean of the highest 9 scores is 47. For the entire group of 10 students, the maximum possible mean exceeds the minimum possible mean by
correct answer:- 2
Question 54
The value of $$1^3-2^3+3^3-4^3......................-100^3$$ is
correct answer:- 1
Question 55
What is 7330th term in the sequence 2, 2, 4, 4, 4, 4, 6, 6, 6, 6, 6, 6, 8, . . . . . is?
correct answer:- 172
Question 56
$$4x^{\sqrt{\ x}^{\sqrt{\ x}^{\sqrt{\ x}^{.^{.^{.^{.^{.\infty\ }}}}}}}}\ =\ 0.0625$$. What is the value of x?
correct answer:- 2
Question 57
In how many ways can a pair of integers (x , a) be chosen such that $$x^{2}-2\mid x\mid+\mid a-2\mid=0$$ ?
correct answer:- 4
Question 58
The area of the region satisfying the inequalities $$\mid x\mid-y\leq1,y\geq0$$ and $$y\leq1$$ is
correct answer:- 3
Question 59
The average of 33 consecutive 3 digit even numbers increases by 6 if the digits of 30th number in series are reversed. If digits of the 30th term are in strictly increasing or strictly decreasing order and hundreds digits of all numbers are the same, what is the sum of digits of the 3rd term in series?
correct answer:- 2
Question 60
Let the m-th and n-th terms of a geometric progression be $$\frac{3}{4}$$ and 12. respectively, where $$m < n$$. If the common ratio of the progression is an integer r, then the smallest possible value of $$r + n - m$$ is
correct answer:- 4
Question 61
f is a function for which f(1)= 1 and f(x) = 2x + f(x - 1) for each natural number x$$\geq$$2. Find f(31)
correct answer:- 4
Question 62
How many natural numbers $$x$$ exist such that, $$x^2+2x+33$$ is divisible by $$x+3$$?
correct answer:- 3
Question 63
If $$x=8-\sqrt{32}$$ and $$y=2+\sqrt{2}$$, then $$\left(x+\frac{1}{y}\right)^2$$ is given by:
correct answer:- 4
Question 64
If a,b are two positive integers such that $$2^{a+3}+3^{b-2}=145$$ and $$2^{2a+1}+3^{2b-7}=371$$, then find the value of $$2^{3a-5}+3^{b-1}$$
correct answer:- 1
Question 65
If $$(a^{\log_{b}{x}})^2 - 5x^{\log_{b}{a}} + 6$$ = 0 where $$a > 1, b > 1$$ and $$a$$ is not equal to $$b$$, then the value of $$x$$ can be
correct answer:- 2
Question 66
If $$\left(3x+y+z+2\right)^2+\left(2x+3y+3z-22\right)^2+\left(x-4y+2z+14\right)^2\ =\ 0$$, Find x-y+z if x,y,z are real?
correct answer:- 3
Question 67
If $$\log_{2}[3+\log_{3} \left\{4+\log_{4}(x-1) \right\}]-2=0$$ then 4x equals
correct answer:- 5
Question 68
For x, y>0, find the value of x, if $$\log_{0.5}x+\log_4y\ =-1$$ and xy=4?
correct answer:- 1
Question 69
A square ABCD in inscribed inside a circle. A circle is inscribed in the square ABCD. This process is repeated infinitely. What is the sum of areas of all the circles, if the radius of the first circle is 5cm?
correct answer:- 3
Question 70
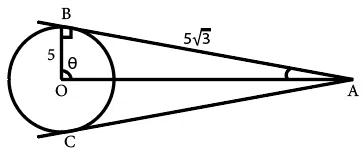
AB and AC are tangents to the circle with centre O. If the radius of the circle is 5 and length of the tangent is $$ 5\sqrt{3}$$, what is the area of the shaded region?

correct answer:- 1
Question 71
In given figure parallelogram MNQR has area 74 sq. m. If S is the midpoint of RQ, find the area of NTQ?
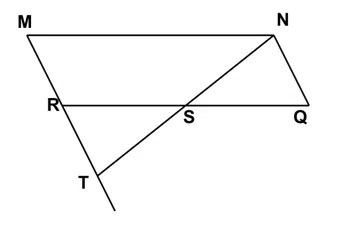
correct answer:- 3
Question 72
A wedding stage is a square of side 10 metres each. At a corner, a triangular section of the stage is cordoned off using a rope in a straight line. If the length of the rope is 6 metres, what is the maximum area which can be cordoned off in the triangle?
correct answer:- 3
Question 73
On a square cardboard of length 10 cm, two identical circles of radius 2 cm are drawn such that the two centres and the two points of intersection of the circle form a square. Find the total area of the cardboard covered by the two circles?
correct answer:- 4
Question 74
A paper is in the shape of a sector of a circle of radius $$6+4\sqrt{3}$$ cm such that the central angle is 120$$^{\circ\ }$$. Now a circle is drawn on this paper. What is the maximum possible radius of this circle?
correct answer:- 4
Question 75
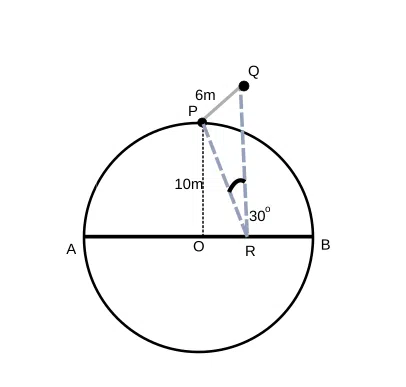
A walking track AB is the diameter of a circular park of radius 10 m. A pole of height 6 m is standing on the circumference of the circular park and it subtends equal angles at A and B. A point R lies on the line AB and the pole subtends 30$$\degree$$ at R. What is the distance of the point R from the center?
correct answer:- 1
Question 76
Balu digs a cylindrical well in his backyard. Just the top surface of the ground (sand) is exposed to the air initially. He heaps the sand excavated in the form of a cone such that the diameter of the well is equal to the diameter of the heap of sand. If the amount of sand exposed to the air has increased by 25% and the diameter of the well is 'n' times the depth of the well, the value of 'n' is
correct answer:- 8
Question 77
Three discs are placed on a bigger disc table, such that the smaller discs touch each other and the edges of the table. What is the area of the shaded region?
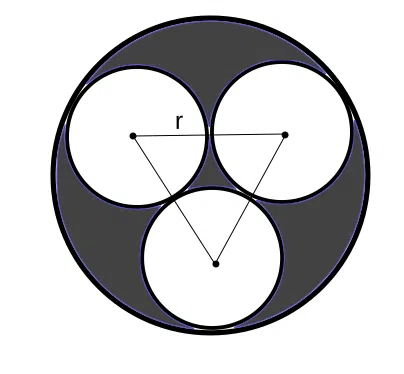
correct answer:- 2
Question 78
In the figure, ABC is an equilateral triangle. Circles with centers P, Q and R are drawn in such a way that they touch the big circle and the sides of the triangle and are of the maximum possible radius. The radius of the big circle is 8 cm. Find the area of triangle PQR.
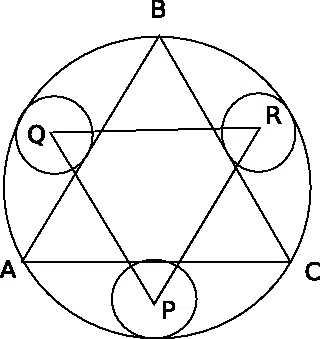
correct answer:- 3
Question 79
If the ratio of an internal angle of a regular polygon of n sides to that of a regular polygon of m sides is 3:4, find out the sum of m and n. Enter -1 if it cannot be determined.
correct answer:- -1
Question 80
In the given rectangle, the midpoints of each side are joined to meet at T. If the area of quadrilaterals TRCQ and STPA are 43 $$cm^2$$ and 17 $$cm^2$$, then what is the sum of the areas of $$\triangle\ SDR$$ and $$\triangle\ QCR$$
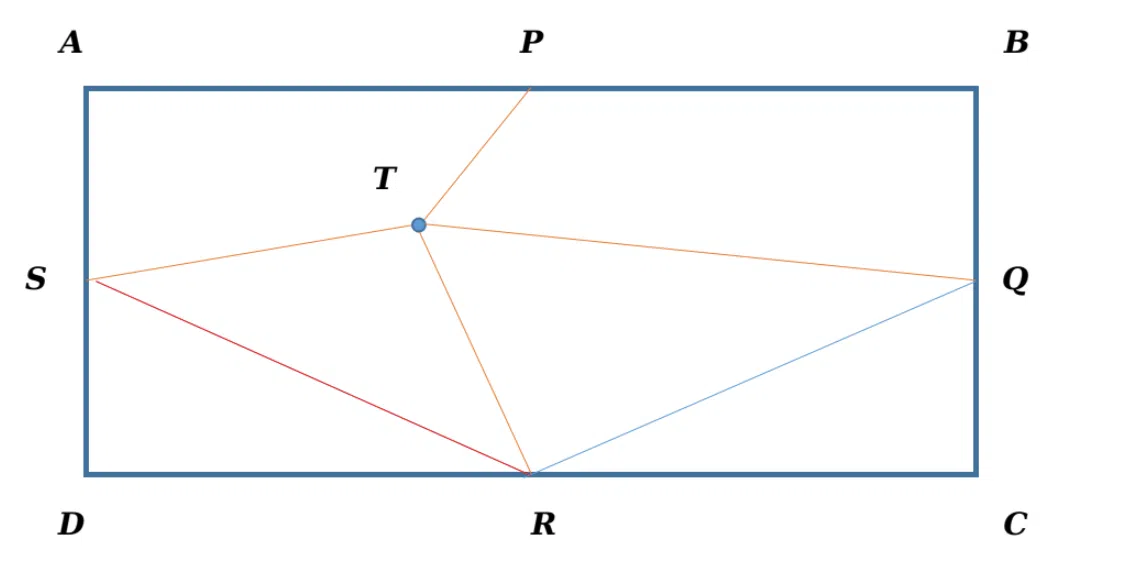
correct answer:- 30
Question 81
An equilateral triangle ABC of side 12 cm is divided by two parallel lines such that the lines IJ and DE cut side AB and CB in ratio 1:1:2.
If F is the midpoint of side AC, what is the area of the shaded region?
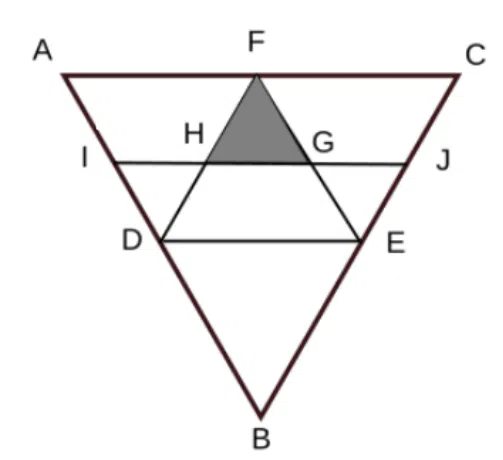
correct answer:- 4
Question 82
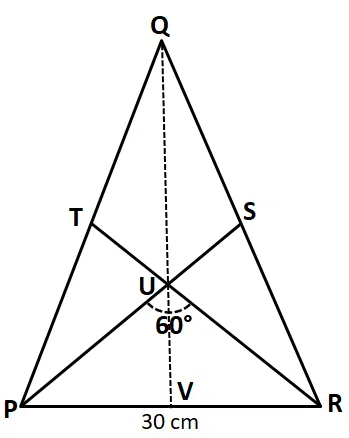
A triangle PQR is drawn such a way that PR = 30 cm and PQ = QR. Two medians are drawn from vertices P and R such that they meet QR and PQ at points S and T respectively. If U is the intersecting point of both the medians and $$\angle$$ PUR = 60°, then find out the area (cm$$^2$$) of triangle PQR.
correct answer:- 5
Question 83
There are 10 train stops between Hyderabad and Vizag. How many types of tickets should be printed to service all kinds of passengers travelling either way on the train?
correct answer:- 1
Question 84
For a natural number X, P(X) represents the probability that a palindrome natural number (chosen randomly) less than X is divisible by 11. Then,
correct answer:- 2
Question 85
If the coefficient of $$x^8$$ in the expansion $$(px^2+\frac{1}{qx})^{13}$$ equals the coefficient of $$x^{-8}$$ in $$(px-\frac{1}{qx^2})^{13}$$, what is the relationship between p and q?
correct answer:- 3
Question 86
Two dices are thrown simultaneously, what is the probability that the sum of the numbers that turn up is less than 9?
correct answer:- 4
Question 87
The circumference of a circle contains 16 equally spaced points. If 3 points out of these 16 points are selected randomly, the probability that the 3 points will form the vertices of an obtuse angled triangle is
correct answer:- 4
Question 88
A toddler is positioned at (0, 0) in x-y plane. He can move by either 1 unit or 3 units at a time in any of x and y directions. If a toy is stationed at (5, 5), then in how many ways he can reach to the toy given that he moves closer to the toy in each step that he takes.
correct answer:- 768
Question 89
ABC Paints Ltd. is planning to create different combination of dyes. The research team has decided they will be using five different green dyes, three different red dyes and four different blue dyes. How many combinations of dyes can be created by ABC Paints Ltd., by including at least one blue and one green dye?
correct answer:- 2
Question 90
How many 4-digit numbers, each greater than 1000 and each having all four digits distinct, are there with 7 coming before 3?
correct answer:- 315
Question 91
What is the reminder when $$17^{128}$$ is divided by 21?
correct answer:- 2
Question 92
The sum of four consecutive two digit even numbers is a perfect square. How such quartets are possible?
correct answer:- 3
Question 93
Rita has a tool which will give the LCM of two numbers. What is the minimum number of times she should run the tool to calculate the LCM of any 20 numbers?
correct answer:- 19
Question 94
How many natural number solutions exist for the equation 1/X + 5/Y = 1/10 if Y < 70
correct answer:- 4
Question 95
Let m and n be natural numbers such that n is even and $$0.2<\frac{m}{20},\frac{n}{m},\frac{n}{11}<0.5$$. Then $$m-2n$$ equals
correct answer:- 2
Question 96
What is that total number of factors of $$882000$$, which have exactly one zero at the end?
correct answer:- 54
Question 97
In a school, 200 students play at least one of Football, Cricket and Hockey. 120 students play Cricket, 60 students play Football and 80 students play Hockey. 20 students play all the three games. Find the number of students that play at least two sports.
correct answer:- 3
Question 98
50 students attempted the midterm tests of class 5th, the midterm consists of 4 subjects English, Hindi, Maths and Science. The number of students passed in these subjects is 35,45,25 and 30. What is the maximum number of students who have passed in exactly one subject?
correct answer:- 20
Question 99
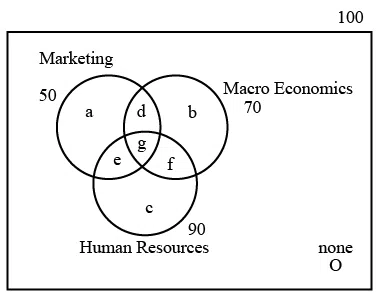
An MBA class 100 students and every student has to choose at least 1 elective amongst the three: marketing, macroeconomics and human resources. 50% of the students chose marketing, 70% of the students chose macroeconomics and 90% chose human resources. Find the minimum no. of students who chose 3 electives?
correct answer:- 1
Question 100
Out of 400 students of an Engineering college, 220 students are giving GRE, 300 students are giving CAT and 50 students are giving GMAT. If it is known that all the students are taking atleast one exam, what is the maximum possible number of students who are giving all three exams?
correct answer:- 4