CAT 2024 Slot 2 Question Paper
For the following questions answer them individually
CAT 2024 Slot 2 - Question 61
If $$m$$ and $$n$$ are natural numbers such that $$n > 1$$, and $$m^n = 2^{25} \times 3^{40}$$, then $$m - n$$ equals
CAT 2024 Slot 2 - Question 63
If x and y are real numbers such that $$4x^2 + 4y^2 - 4xy - 6y + 3 = 0$$, then the value of $$(4x + 5y)$$ is
789
456
123
0.-
Clear All
CAT 2024 Slot 2 - Question 64
If $$(x + 6\sqrt{2})^{\cfrac{1}{2}} - (x - 6\sqrt{2})^{\cfrac{1}{2}} = 2\sqrt{2}$$, then x equals
789
456
123
0.-
Clear All
CAT 2024 Slot 2 - Question 65
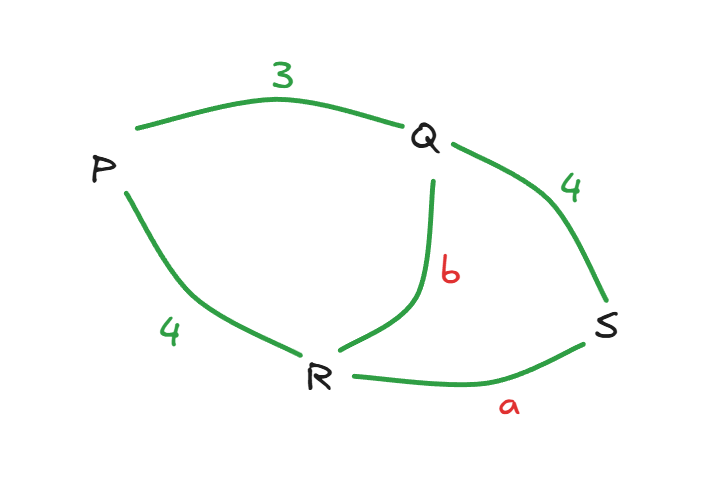
P, Q, R and S are four towns. One can travel between P and Q along 3 direct paths, between Q and S along 4 direct paths, and between P and R along 4 direct paths. There is no direct path between P and S, while there are few direct paths between Q and R, and between R and S. One can travel from P to S either via Q, or via R, or via Q followed by R, respectively, in exactly 62 possible ways. One can also travel from Q to R either directly, or via P, or via S, in exactly 27 possible ways. Then, the number of direct paths between Q and R is
789
456
123
0.-
Clear All
CAT 2024 Slot 2 - Question 66
If x and y satisfy the equations $$\mid x \mid + x + y = 15$$ and $$x + \mid y \mid - y = 20$$, then $$(x - y)$$ equals
CAT 2024 Slot 2 - Question 67
A vessel contained a certain amount of a solution of acid and water. When 2 litres of water was added to it, the new solution had 50% acid concentration. When 15 litres of acid was further added to this new solution, the final solution had 80% acid concentration. The ratio of water and acid in the original solution was
CAT 2024 Slot 2 - Question 68
The sum of the infinite series $$\cfrac{1}{5}\left(\cfrac{1}{5} - \cfrac{1}{7}\right) + \left(\cfrac{1}{5}\right)^2 \left(\left(\cfrac{1}{5}\right)^2 - \left(\cfrac{1}{7}\right)^2\right) + \left(\cfrac{1}{5}\right)^3 \left(\left(\cfrac{1}{5}\right)^3 - \left(\cfrac{1}{7}\right)^3\right) + ......$$ is equal to
Two Factor Authentication
Incase of any issue contact support@cracku.in
CAT Quant Questions | CAT Quantitative Ability
CAT DILR Questions | LRDI Questions For CAT
CAT Verbal Ability Questions | VARC Questions For CAT
Also Read
Frequently Asked Questions
You can download the CAT 2024 Slot 2 PDF with solutions directly from Cracku’s website.
Yes, detailed video solutions are available for every question in VARC, LRDI, and Quant.
Practicing with the Slot 2 paper improves problem-solving, time management, and familiarity with actual CAT questions.
The overall level was moderate to difficult, with VARC being slightly tricky, LRDI challenging, and Quant moderate.
Yes, you can download the Slot 2 question paper PDF with video solutions for free from Cracku.