CAT 2017 Slot 2 Question Paper
For the following questions answer them individually
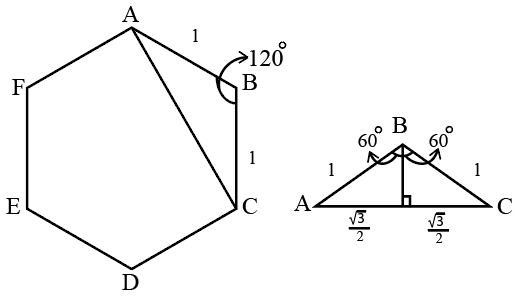
CAT 2017 Slot 2 - Question 81
Let ABCDEF be a regular hexagon with each side of length 1 cm. The area (in sq cm) of a square with AC as one side is
CAT 2017 Slot 2 - Question 82
The base of a vertical pillar with uniform cross section is a trapezium whose parallel sides are of lengths 10 cm and 20 cm while the other two sides are of equal length. The perpendicular distance between the parallel sides of the trapezium is 12 cm. If the height of the pillar is 20 cm, then the total area, in sq cm, of all six surfaces of the pillar is
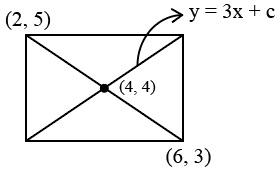
CAT 2017 Slot 2 - Question 83
The points (2, 5) and (6, 3) are two end points of a diagonal of a rectangle. If the other diagonal has the equation y =3x+c,then c is
CAT 2017 Slot 2 - Question 84
ABCD is a quadrilateral inscribed in a circle with centre O such that O lies inside the quadrilateral. If $$\angle COD = 120$$ degrees and $$\angle BAC = 30$$ degrees, then the value of $$\angle BCD$$ (in degrees) is
789
456
123
0.-
Clear All
CAT 2017 Slot 2 - Question 85
If three sides of a rectangular park have a total length 400 ft, then the area of the park is maximum when the length (in ft) of its longer side is
789
456
123
0.-
Clear All
CAT 2017 Slot 2 - Question 86
Let P be an interior point of a right-angled isosceles triangle ABC with hypotenuse AB. If the perpendicular distance of P from each of AB,BC,and CA is $$4(\sqrt{2}-1)$$ cm,then the area, in sq cm, of the triangle ABC is
789
456
123
0.-
Clear All
CAT 2017 Slot 2 - Question 87
If the product of three consecutive positive integers is 15600 then the sum of the squares of these integers is
CAT 2017 Slot 2 - Question 88
If x is a real number such that $$\log_{3}5= \log_{5}(2 + x)$$, then which of the following is true?
CAT 2017 Slot 2 - Question 89
Let $$f(x) = x^{2}$$ and $$g(x) = 2^{x}$$, for all real x. Then the value of f[f(g(x)) + g(f(x))] at x = 1 is
CAT 2017 Slot 2 - Question 90
The minimum possible value of the sum of the squares of the roots of the equation $$x^2+(a+3)x-(a+5)=0 $$ is
Two Factor Authentication
Incase of any issue contact support@cracku.in