From a triangle ABC with sides of lengths 40 ft, 25 ft and 35 ft, a triangular portion GBC is cut off where G is the centroid of ABC. The area, in sq ft, of the remaining portion of triangle ABC is
The lengths are given as 40, 25 and 35.
The perimeter = 100
Semi-perimeter, s = 50
Area = $$ \sqrt{50 * 10 * 25 * 15}$$ = $$250\sqrt{3}$$
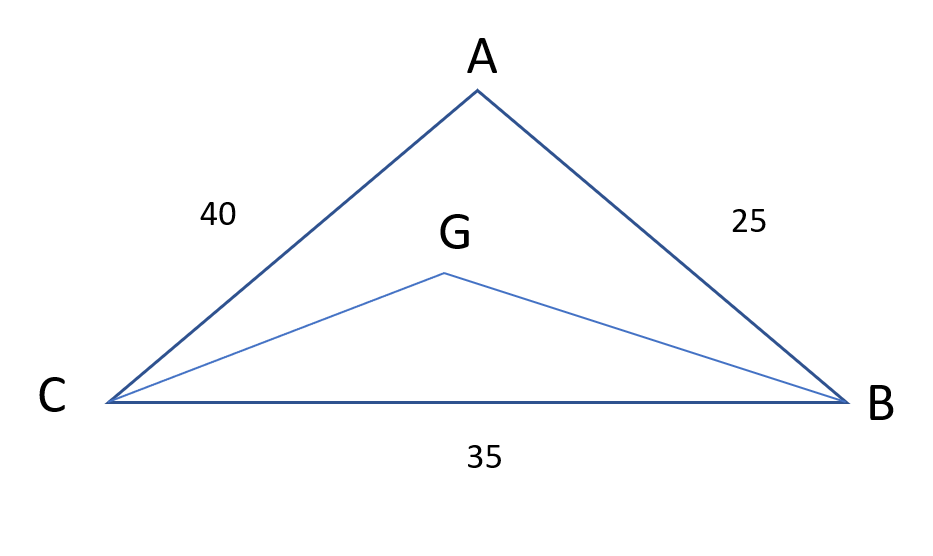
The triangle formed by the centroid and two vertices is removed.
Since the cenroid divides the median in the ratio 2 : 1
The remaining area will be two-thirds the area of the original triangle.
Remaining area = $$\frac{2}{3} * 250\sqrt{3}$$ = $$\frac{500}{\sqrt{3}}$$
Video Solution

Your Doubts
Create a FREE account and get:
- All Quant CAT complete Formulas and shortcuts PDF
- 38+ CAT previous year papers with video solutions PDF
- 5000+ Topic-wise Previous year CAT Solved Questions for Free





