How many members are there in the club?

We can represent People by points and relation of being friends by joining those points . so a set of people and their relations can be represented by a graph .
1. No two friends have a common friend .
2.Any two non friends have exactly 2 common friends .

Consider any point X 
let say there are exactly m points $$\ A_1,\ A_2,A_3.....A_m\ \ $$ connected with X .None of these points can be connected with each other , therefore corresponding to every pair Ai , Aj there have to be exactly two points connected to both.
One is X, the other is Bij.This has to be different values for i,j . This has to be the complete graph i.e a point x , a point connected to X or a point connected to Ai .
There can be no point unconnected with every one of these points . If X and P are unconnected they have to have two common friends .
All friends of X are included in $$\ A_1,\ A_2,A_3.....A_m\ \ $$
So P has to be connected with some of A's . Also there can be no other point connected with any Ai .If there is a point B it can't be connected to any Aj for it would be then Bij and X and B will have 1 common friend
so the points in graphs are :
$$X,\ A_1,\ A_2,A_3.....A_m\ B_{12\ },\ B_{13}......B_{\left(m-1\right)m}\ \ $$
The number of points is
n = 1+m +(m)(m-1)/2
some values of m, n are given below :

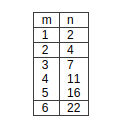
we have to consider m =3,4,5
When m =3
we can't provide friend to B12 so m cannot be 3
m =4
we get

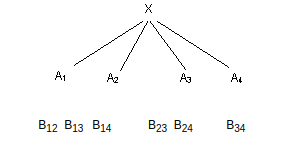
Take B12 , he has two friends A1 and A2 , but we cannot provide two more friends among Bij's . Only B34 is available .

Consider m =5 

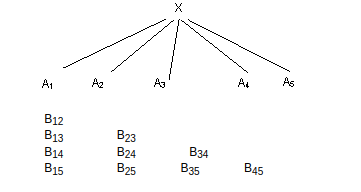
B12 has A1 and A2 and we have to provide three more they are (B34 , B35 and B45)
Hence m =5 and n =16
so we get 16 members in the group