XAT 2019 Question Paper
For the following questions answer them individually
XAT 2019 - Question 51
If $$\sqrt[3]{7^a\times 35^{b+1} \times 20^{c+2}}$$ is a whole number then which one of the statements below is consistent with it?
XAT 2019 - Question 52
A gold ingot in the shape of a cylinder is melted and the resulting molten metal molded into a few identical conical ingots. If the height of each cone is half the height of the original cylinder and the area of the circular base of each cone is one fifth that of the circular base of the cylinder, then how many conical ingots can be made?
XAT 2019 - Question 53
Given that a and b are integers and that $$5x+2\sqrt{7}$$ is a root of the polynomial $$x^2 - ax + b + 2\sqrt{7}$$ in $$x$$, what is the value of b?
XAT 2019 - Question 54
An article is marked x% above the cost price. A discount of $$\frac{2}{3}$$x% is given on the marked price. If the profit is 4% of the cost price and the value of x lies between 25 and 50, then the value of 50% of x is?
XAT 2019 - Question 55
A computer is sold either for Rs.19200 cash or for Rs.4800 cash down payment together with five equal monthly installments. If the rate of interest charged is 12% per annum compounded anually, then the amount of each installment (nearest to a rupee) is:
XAT 2019 - Question 56
When opening his fruit shop for the day a shopkeeper found that his stock of apples could be perfectly arranged in a complete triangular array: that is, every row with one apple more than the row immediately above, going all the way up ending with a single apple at the top.
During any sales transaction, apples are always picked from the uppermost row, and going below only when that row is exhausted.
When one customer walked in the middle of the day she found an incomplete array in display having 126 apples totally. How many rows of apples (complete and incomplete) were seen by this customer? (Assume that the initial stock did not exceed 150 apples.)
XAT 2019 - Question 57
Let P be the point of intersection of the lines
3x + 4y = 2a and 7x + 2y = 2018
and Q the point of intersection of the lines
3x + 4y = 2018 and 5x + 3y = 1
If the line through P and Q has slope 2, the value of a is:
XAT 2019 - Question 58
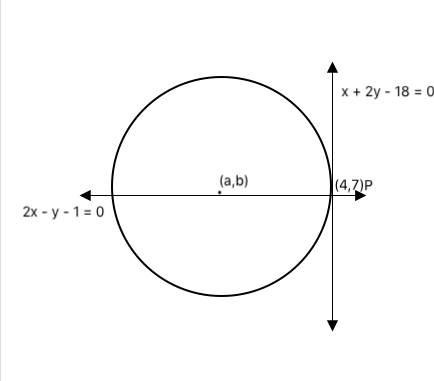
Let C be a circle of radius $$\sqrt{20}$$ cm. Let L1, L2 be the lines given by 2x − y −1 = 0 and x + 2y−18 = 0, respectively. Suppose that L1 passes through the center of C and that L2 is tangent to C at the point of intersection of L1 and L2. If (a,b) is the center of C, which of the following is a possible value of a + b?
XAT 2019 - Question 59
$$\frac{log (97-56\sqrt{3})}{log \sqrt{7+4\sqrt{3}}}$$ equals which of the following?
XAT 2019 - Question 60
In the trapezium ABCD the sides AB and CD are parallel. The value of $$\frac{sin \angle{BAC}}{sin \angle{BAD}}$$ is

Two Factor Authentication
Incase of any issue contact support@cracku.in






.webp)