XAT 2016 Question Paper - QUANT
For the following questions answer them individually
XAT 2016 - QUANT - Question 50
In the figure below, AB = AC = CD. If ADB = 20°, what is the value of BAD?

XAT 2016 - QUANT - Question 51
In an amusement park, a visitor gets to ride on three different rides (A, B and C) for free. On a particular day 77 opted for ride A, 55 opted for B and 50 opted for C; 25 visitors opted for both A and C, 22 opted for both A and B, while no visitor opted for both B and C. 40 visitors did not opt for ride A and B, or both. How many visited the amusement park on that day?
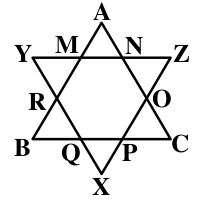
XAT 2016 - QUANT - Question 52
$$\triangle$$ABC and $$\triangle$$XYZ are equilateral triangles of 54 cm sides. All smaller triangles like $$\triangle$$ANM, $$\triangle$$OCP, $$\triangle$$QPX etc. are also equilateral triangles. Find the area of the shape MNOPQRM.
XAT 2016 - QUANT - Question 53
Akhtar plans to cover a rectangular floor of dimensions 9.5 meters and 11.5 meters using tiles. Two types of square shaped tiles are available in the market. A tile with side 1 meter costs Rs. 100 and a tile with side 0.5 meters costs Rs. 30. The tiles can be cut if required. What will be the minimum cost of covering the entire floor with tiles?
XAT 2016 - QUANT - Question 54
Anita, Biplove, Cheryl, Danish, Emily and Feroze compared their marks among themselves. Anita scored the highest marks, Biplove scored more than Danish. Cheryl scored more than at least two others and Emily had not scored the lowest.
Statement I: Exactly two members scored less than Cheryl.
Statement II: Emily and Feroze scored the same marks.
Which of the following statements would be sufficient to identify the one with the lowest marks?
XAT 2016 - QUANT - Question 55
Rani bought more apples than oranges. She sells apples at Rs. 23 apiece and makes 15% profit. She sells oranges at Rs. 10 a piece and makes 25% profit. If she gets Rs. 653 after selling all the apples and oranges, find her profit percentage.
XAT 2016 - QUANT - Question 56
Consider the set of numbers {1, 3, $$3^{2}$$, $$3^{3}$$,…...,$$3^{100}$$}. The ratio of the last number and the sum of the remaining numbers is closest to:
XAT 2016 - QUANT - Question 57
f is a function for which f(1)= 1 and f(x) = 2x + f(x - 1) for each natural number x$$\geq$$2. Find f(31)
XAT 2016 - QUANT - Question 58
Two numbers in the base system B are 2061$$_{B}$$ and 601$$_{B}$$. The sum of these two numbers in decimal system is 432. Find the value of 1010$$_B$$ in decimal system.
XAT 2016 - QUANT - Question 59
A water tank has M inlet pipes and N outlet pipes. An inlet pipe can fill the tank in 8 hours while an outlet pipe can empty the full tank in 12 hours. If all pipes are left open simultaneously, it takes 6 hours to fill the empty tank. What is the relationship between M and N?
XAT 2016 - QUANT - Question 60
Company ABC starts an educational program in collaboration with Institute XYZ. As per the agreement, ABC and XYZ will share profit in 60 : 40 ratio. The initial investment of Rs.100,000 on infrastructure is borne entirely by ABC whereas the running cost of Rs. 400 per student is borne by XYZ. If each student pays Rs. 2000 for the program find the minimum number of students required to make the program profitable, assuming ABC wants to recover its investment in the very first year and the program has no seat limits.
XAT 2016 - QUANT - Question 61
Study the figure below and answer the question:

Four persons walk from Point A to Point D following different routes. The one following ABCD takes 70 minutes. Another person takes 45 minutes following ABD. The third person takes 30 minutes following route ACD. The last person takes 65 minutes following route ACBD. IF all were to walk at the same speed, how long will it take to go from point B to point C?
XAT 2016 - QUANT - Question 62
Each day on Planet M is 10 hours, each hour 60 minutes and each minute 40 seconds. The inhabitants of Planet M use 10 hour analog clock with an hour hand, a minute hand and a second hand. If one such clock shows 3 hours 42 minutes and 20 seconds in a mirror what will be the time in Planet M exactly after 5 minutes?
XAT 2016 - QUANT - Question 63
a, b, c are integers, |a| ≠ |b| ≠|c| and -10 ≤ a, b, c ≤ 10. What will be the maximum possible value of [abc - (a + b + c)]?
XAT 2016 - QUANT - Question 64
A square piece of paper is folded three times along its diagonal to get an isosceles triangle whose equal sides are 10 cm. What is the area of the unfolded original piece of paper?
XAT 2016 - QUANT - Question 65
The difference between the area of the circumscribed circle and the area of the inscribed circle of an equilateral triangle is 2156 sq. cm. What is the area of the equilateral triangle?
Assume that $$\pi=\frac{22}{7}$$
XAT 2016 - QUANT - Question 66
A person standing on the ground at point A saw an object at point B on the ground at a distance of 600 meters. The object started flying towards him at an angle of 30° with the ground. The person saw the object for the second time at point C flying at 30° angle with him. At point C, the object changed direction and continued flying upwards. The person saw the object for the third time when the object was directly above him. The object was flying at a constant speed of 10 kmph.

Find the angle at which the object was flying after the person saw it for the second time. You may use additional statement(s) if required.
Statement I: After changing direction the object took 3 more minutes than it had taken before.
Statement II: After changing direction the object travelled an additional 200√3 meters.
Which of the following is the correct option?
XAT 2016 - QUANT - Question 67
For two positive integers a and b, if $$(a + b)^{(a + b)}$$ is divisible by 500, then the least possible value of a $$\times$$ b is:
XAT 2016 - QUANT - Question 68
Pradeep could either walk or drive to office. The time taken to walk to the office is 8 times the driving time. One day, his wife took the car making him walk to office. After walking 1km, he reached a temple when his wife called to say that he can now take the car. Pradeep figure that continuing to walk to the office will take as long as walking back home and then driving to the office. Calculate the distance between the temple and the office.
XAT 2016 - QUANT - Question 69
If a, b and c are 3 consecutive integers between -10 to +10 (both inclusive), how many integer values are possible for the expression?
$$\frac{a^3+b^3+c^3+3abc}{(a+b+c)^2}$$=?
XAT 2016 - QUANT - Question 70
In the figure below, two circular curves y and x create 60° and 90° angles with their respective centres. If the length of the bottom curve Y is 10$$\pi\ $$, find the length of the other curve.

XAT 2016 - QUANT - Question 71
ABCD is a quadrilateral such that AD = 9 cm, BC = 13 cm and $$\angle$$DAB = $$\angle$$BCD = 90°. P and Q are two points on AB and CD respectively, such that DQ : BP = 1 : 2 and DQ is an integer. How many values can DQ take, for which the maximum possible area of the quadrilateral PBQD is 150 sq.cm?
Study the data given in the table below and answer the question that follow:

All figures are in percentage
Based on survey of ‘shop types’ Kamath categorized Indian states into four geographical regions as shown in the table above. His boss felt that the categorization was inadequate since important labels were missing. Kamath argued that no further labels are required to interpret the data.
XAT 2016 - QUANT - Question 72
A consultant observing the data made the following two inferences:
Inference I: The number of Grocers per-thousand-population is the highest in North India.
Inference II: The number of Cosmetic per-thousand-population is the highest in South India.
Which of following options is DEFINITELY correct?
XAT 2016 - QUANT - Question 73
The average size of Food Shops in East India was twice that of Food Shops in West India. Which of the following cannot be inferred from the above data?
XAT 2016 - QUANT - Question 74
Bala collected the same data five years after Kamath, using the same categorization.
Which of the following statements can DEFINITELY be concluded?
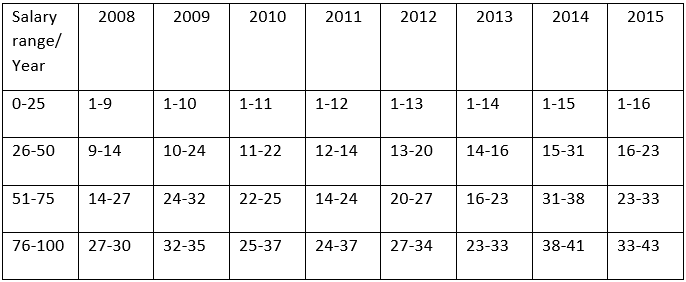
Study the graph below and answer the questions that follow:
This graph depicts the last eight years’ annual salaries (in Rs. lacs.) offered to student during campus placement. Every year 100 students go through placement process. However, at least one of them fails to get placed. The salaries of all unplaced students are marked zero and represented in the graph.

The bold line in the graph presents Mean salaries at various years.
XAT 2016 - QUANT - Question 75
In which year were a maximum number of students offered salaries between Rs. 20 to Rs.30 lacs(both inclusive)?
XAT 2016 - QUANT - Question 76
Identify the years in which the annual median salary is higher by at least 60% than the average salary of the preceding year?
XAT 2016 - QUANT - Question 77
Identify the number of years in which the difference between the average salaries of the top 25% and the bottom 25% is more than Rs. 20 lacs:
XAT 2016 - QUANT - Question 78
If the average salary is computed excluding students with no offers, in how many years will the new average salary be greater than the existing median salary? Refer the table below for number of students without offers.

Two Factor Authentication
Incase of any issue contact support@cracku.in




.PNG)