CAT 2025 Slot 1 Question Paper
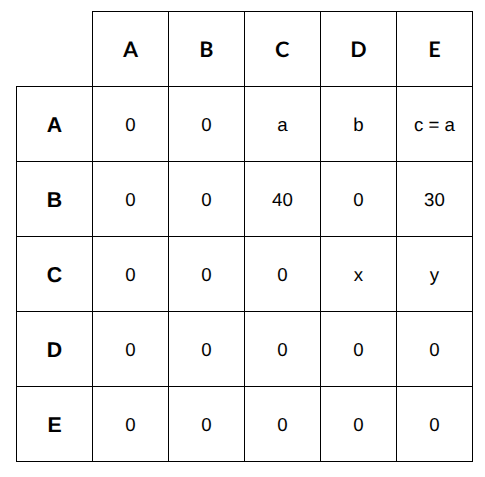
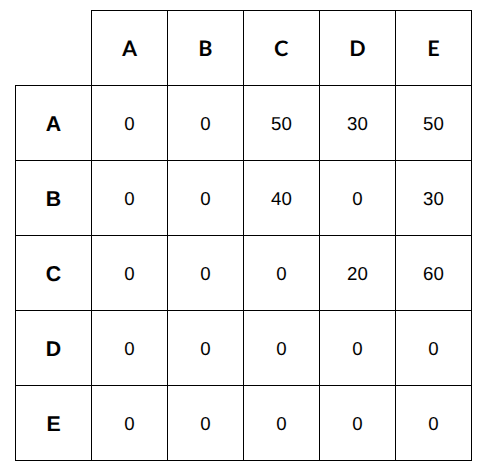
A train travels from Station A to Station E, passing through stations B, C, and D, in that order. The train has a seating capacity of 200. A ticket may be booked from any station to any other station ahead on the route, but not to any earlier station.
A ticket from one station to another reserves one seat on every intermediate segment of the route. For example, a ticket from B to E reserves a seat in the intermediate segments B - C, C - D, and D - E.
The occupancy factor for a segment is the total number of seats reserved in the segment as a percentage of the seating capacity. The total number of seats reserved for any segment cannot exceed 200.
The following information is known.
1. Segment C - D had an occupancy factor of 95%. Only segment B - C had a higher occupancy factor.
2. Exactly 40 tickets were booked from B to C and 30 tickets were booked from B to E.
3. Among the seats reserved on segment D - E, exactly four-sevenths were from stations before C.
4. The number of tickets booked from A to C was equal to that booked from A to E, and it was higher than that from B to E.
5. No tickets were booked from A to B, from B to D and from D to E.
6. The number of tickets booked for any segment was a multiple of 10.
CAT 2025 Slot 1 - Question 41
What is the difference between the number of tickets booked to Station C and the number of tickets booked to Station D?
789
456
123
0.-
Clear All
CAT 2025 Slot 1 - Question 42
How many tickets were booked to travel in exactly one segment?
789
456
123
0.-
Clear All
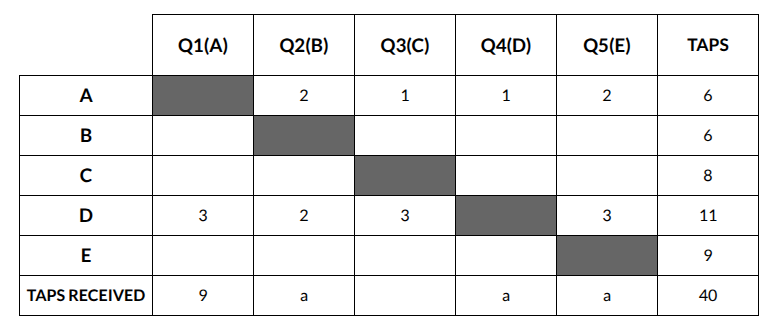
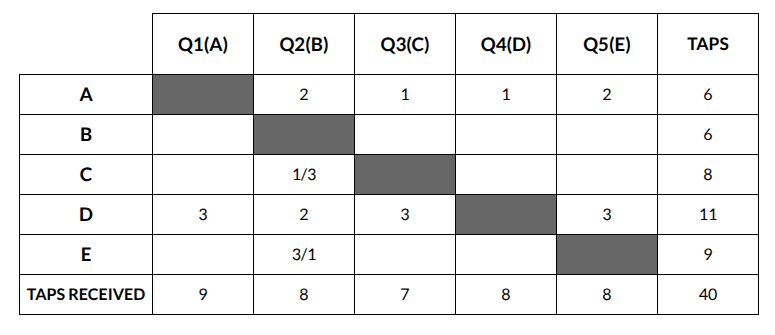
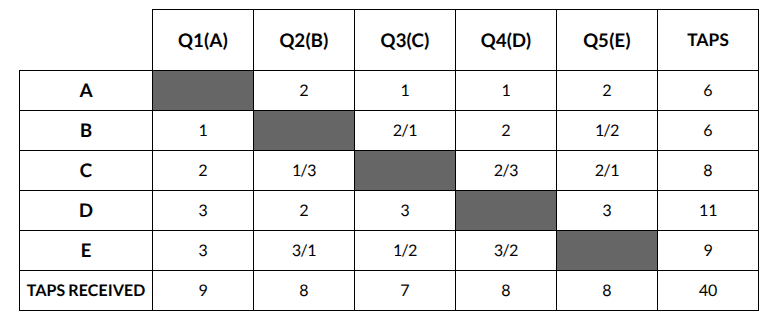
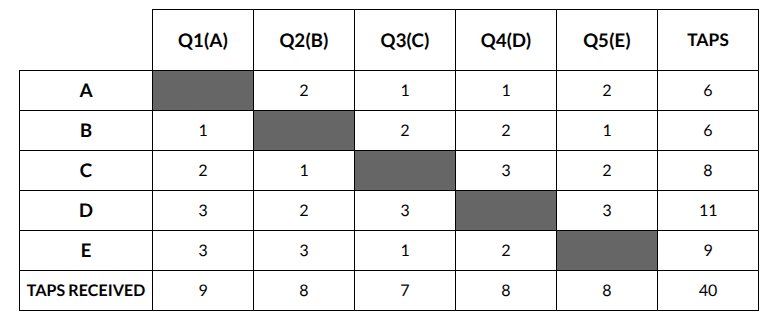
Alia, Badal, Clive, Dilshan, and Ehsaan played a game in which each asks a unique question to all the others and they respond by tapping their feet, either once or twice or thrice. One tap means “Yes”, two taps mean “No”, and three taps mean “Maybe”.
A total of 40 taps were heard across the five questions. Each question received at least one “Yes”, one “No”, and one “Maybe.”
The following information is known.
1. Alia tapped a total of 6 times and received 9 taps to her question. She responded “Yes” to the questions asked by both Clive and Dilshan.
2. Dilshan and Ehsaan tapped a total of 11 and 9 times respectively. Dilshan responded “No” to Badal.
3. Badal, Dilshan, and Ehsaan received equal number of taps to their respective questions.
4. No one responded “Yes” more than twice.
5. No one’s answer to Alia’s question matched the answer that Alia gave to that person’s question. This was also true for Ehsaan.
6. Clive tapped more times in total than Badal.
CAT 2025 Slot 1 - Question 43
How many taps did Clive receive for his question?
789
456
123
0.-
Clear All
CAT 2025 Slot 1 - Question 44
Which two people tapped an equal number of times in total?
CAT 2025 Slot 1 - Question 45
What was Clive’s response to Ehsaan’s question?
CAT 2025 Slot 1 - Question 46
How many “Yes” responses were received across all the questions?
789
456
123
0.-
Clear All
For the following questions answer them individually
CAT 2025 Slot 1 - Question 47
A value of $$c$$ for which the minimum value of $$f(x)=x^{2}-4cx+8c$$ is greater than the maximum value of $$g(x)=-x^{2}+3cx-2c$$, is
CAT 2025 Slot 1 - Question 48
Shruti travels a distance of 224 km in four parts for a total travel time of 3 hours. Her speeds in these four parts follow an arithmetic progression, and the corresponding time taken to cover these four parts follow another arithmetic progression. If she travels at a speed of 960 meters per minute for 30 minutes to cover the first part, then the distance, in meters, she travels in the fourth part is
CAT 2025 Slot 1 - Question 49
In a 3-digit number N, the digits are non-zero and distinct such that none of the digits is a perfect square, and only one of the digits is a prime number. Then, the number of factors of the minimum possible value of N is
789
456
123
0.-
Clear All
CAT 2025 Slot 1 - Question 50
Let $$3\leq x\leq6$$ and $$\left[x^{2}\right] =\left[x\right]^{2}$$ , where $$[x]$$ is the greatest integer not exceeding $$x$$ . If set $$S$$ represents all feasible values of $$x$$, then a possible subset of $$S$$ is