CAT 2017 Slot 1 Question Paper
For the following questions answer them individually
CAT 2017 Slot 1 - Question 81
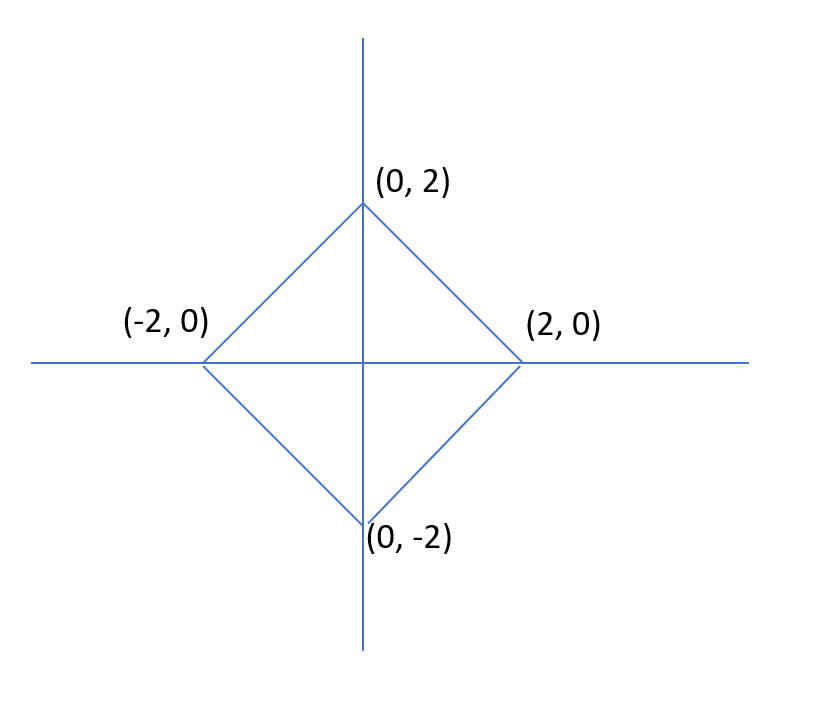
The area of the closed region bounded by the equation
I x I + I y I = 2 in the two-dimensional plane is
CAT 2017 Slot 1 - Question 82
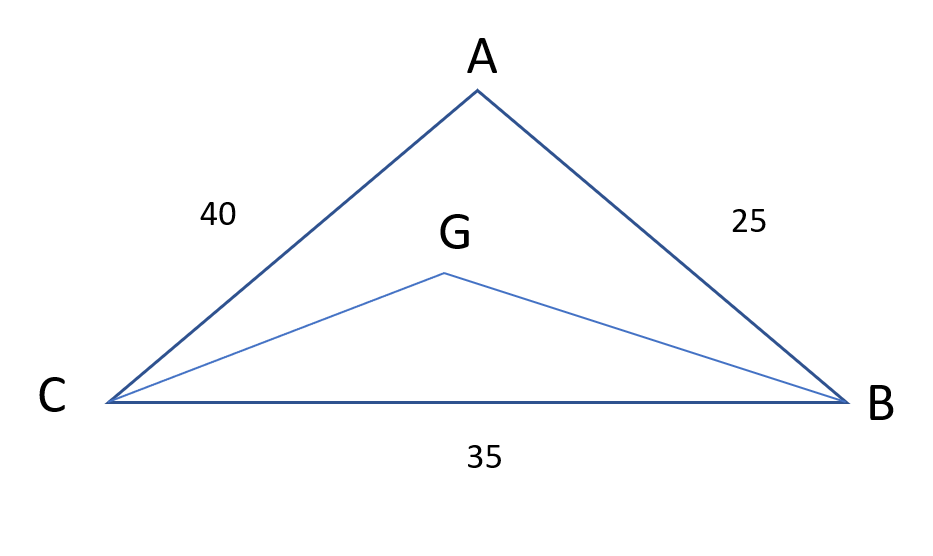
From a triangle ABC with sides of lengths 40 ft, 25 ft and 35 ft, a triangular portion GBC is cut off where G is the centroid of ABC. The area, in sq ft, of the remaining portion of triangle ABC is
CAT 2017 Slot 1 - Question 83
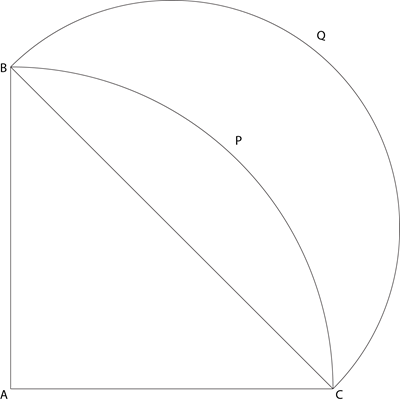
Let ABC be a right-angled isosceles triangle with hypotenuse BC. Let BQC be a semi-circle, away from A, with diameter BC. Let BPC be an arc of a circle centered at A and lying between BC and BQC. If AB has length 6 cm then the area, in sq cm, of the region enclosed by BPC and BQC is
CAT 2017 Slot 1 - Question 84
A solid metallic cube is melted to form five solid cubes whose volumes are in the ratio 1 : 1 : 8 : 27 : 27. The percentage by which the sum of the surface areas of these five cubes exceeds the surface area of the original cube is nearest to
CAT 2017 Slot 1 - Question 85
A ball of diameter 4 cm is kept on top of a hollow cylinder standing vertically. The height of the cylinder is 3 cm, while its volume is $$9\pi$$ cubic centimeters. Then the vertical distance, in cm, of the topmost point of the ball from the base of the cylinder is
789
456
123
0.-
Clear All
CAT 2017 Slot 1 - Question 86
Let ABC be a right-angled triangle with BC as the hypotenuse. Lengths of AB and AC are 15 km and 20 km, respectively. The minimum possible time, in minutes, required to reach the hypotenuse from A at a speed of 30 km per hour is
789
456
123
0.-
Clear All
CAT 2017 Slot 1 - Question 87
Suppose, $$\log_3 x = \log_{12} y = a$$, where $$x, y$$ are positive numbers. If $$G$$ is the geometric mean of x and y, and $$\log_6 G$$ is equal to
CAT 2017 Slot 1 - Question 89
The value of $$\log_{0.008}\sqrt{5}+\log_{\sqrt{3}}81-7$$ is equal to
Two Factor Authentication
Incase of any issue contact support@cracku.in