CAT 2017 Question Paper Slot 1
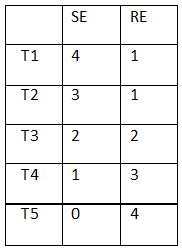
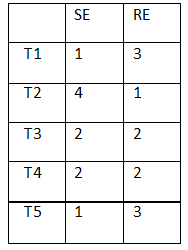
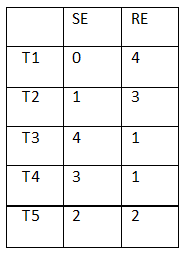
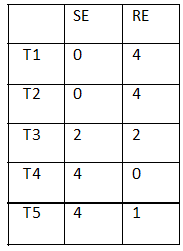
There are 21 employees working in a division, out of whom 10 are special-skilled employees (SE) and the remaining are regular-skilled employees (RE). During the next five months, the division has to complete five projects every month. Out of the 25 projects, 5 projects are "challenging", while the remaining ones are "standard". Each of the challenging projects has to be completed in different months. Every month, five teams — T1 T2, T3, T4 and T5, work on one project each. T1, T2, T3, T4 and T5 are allotted the challenging project in the first, second, third, fourth and fifth month, respectively. The team assigned the challenging project has one more employee than the rest.
In the first month, T1 has one more SE than T2, T2 has one more SE than T3, T 3 has one more SE than T4, and T4 has one more SE than T5. Between two successive months, the composition of the teams changes as follows:
a. The team allotted the challenging project, gets two SE from the team which was allotted the challenging project in the previous month. In exchange, one RE is shifted from the former team to the latter team.
b. After the above exchange, if T1 has any SE and T5 has any RE, then one SE is shifted from T1 to T5, and one RE is shifted from T5 to T1. Also, if T2 has any SE and T4 has any RE, then one SE is shifted from T2 to T4, and one RE is shifted from T4 to T2.
Each standard project has a total of 100 credit points, while each challenging project has 200 credit points. The credit points are equally shared between the employees included in that team.
The number of times in which the composition of team T2 and the number of times in which composition of team T4 remained unchanged in two successive months are:
Which of the following CANNOT be the total credit points earned by any employee from the projects?
One of the employees named Aneek scored 185 points. Which of the following CANNOT be true?
Question Numbers: (55 to 58)
In a square layout of site 5m ~ 5m 25 equal-sized square platforms of different heights are built. The heights (in metre) of individual platforms are as shown below:
Individuals (all of same height) are seated on these platforms. We say an individual A can reach individual B, if all the three following conditions are met;
(i) A and B are In the same row or column
(ii) A is at a lower height than B
(iii) If there is/are any individuals (s) between A and B, such individual(s) must be at a height lower than that of A.
Thus in the table given above, consider the Individual seated at height 8 on 3rd row and 2nd column. He can be reached by four individuals. He can be reached by the individual on his left at height 7, by the two individuals on his right at heights of 4 and 6 and by the individual above at height 5.
Rows in the layout are numbered from top to bottom and columns are numbered from left to right.
Which of the following is true for any individual at a platform of height 1 m in this layout?
A new airlines company is planning to start operations in a country. The company has identified ten different cities which they plan to connect through their network to start with. The flight duration between any pair of cities will be less than one hour. To start operations, the company has to decide on a daily schedule.
The underlying principle that they are working on is the following:
Any person staying in any of these 10 cities should be able to make a trip to any other city in the morning and should be able to return by the evening of the same day.
If the underlying principle is to be satisfied in such a way that the journey between any two cities can be performed using only direct (non-stop) flights, then the minimum number of direct flights to be scheduled is:
Suppose three of the ten cities are to be developed as hubs. A hub is a city which is connected with every other city by direct flights each way, both in the morning as well as in the evening. The only direct flights which will be scheduled are originating and/or terminating in one of the hubs. Then the minimum number of direct flights that need to be scheduled so that the underlying principle of the airline to serve all the ten cities is met without visiting more than one hub during one trip is:
