Question 77
Let ABC be a right-angled triangle with hypotenuse BC of length 20 cm. If AP is perpendicular on BC, then the maximum possible length of AP, in cm, is
Solution
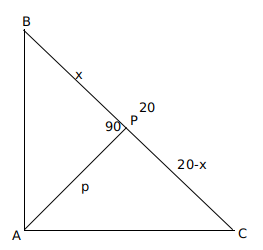

Let p be the length of AP.
It is given that $$\angle\ BAC\ =90\ $$ and $$\angle\ APC\ =90\ $$
Let $$\angle\ ABC\ =\theta\ $$, then $$\angle\ BAP\ =90-\theta\ $$ and $$\angle\ BCA\ =90-\theta\ $$
So $$\angle\ PAC\ =\theta\ $$
Triangles BPA and APC are similar
$$p^2=x\left(20-x\right)$$
We have to maximize the value of p, which will be maximum when x=20-x
x=10
Video Solution

Your Doubts
Ask a Doubt
(know more)
Create a FREE account and get:
- All Quant CAT complete Formulas and shortcuts PDF
- 38+ CAT previous year papers with video solutions PDF
- 5000+ Topic-wise Previous year CAT Solved Questions for Free
CAT Quant Questions | CAT Quantitative Ability
CAT Linear Equations QuestionsCAT Quadratic Equations QuestionsCAT Mensuration QuestionsCAT Remainders QuestionsCAT Number Systems Questions
CAT DILR Questions | LRDI Questions For CAT
CAT Puzzles QuestionsCAT Selection With Condition QuestionsCAT Arrangement QuestionsCAT Truth Lie Concept QuestionsCAT Routes And Networks Questions




