The central park of the city is 40 metres long and 30 metres wide. The mayor wants to construct two roads of equal width in the park such that the roads intersect each other at right angles and the center of the rectangle co-incides with the center of the rectangle formed by the intersection of the two roads . Further, the mayor wants that the area of the two roads to be equal to the remaining area of the park. What should be the width of the roads?
Solution
Let us draw the diagram according to the information given in the questions.
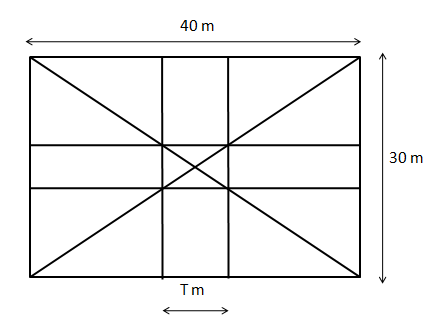
Let us assume that 'T' is the width of the road as shown in the diagram.
Total area covered by road = $$30*T+40*T-T^2$$
Also it is given that the mayor wants that the area of the two roads to be equal to the remaining area of the park.
$$\Rightarrow$$ $$30*T+40*T-T^2$$ = $$\dfrac{30*40}{2}$$
$$\Rightarrow$$ $$T^2-70T+600$$ = $$0$$
$$\Rightarrow$$ $$(T-10)(T-60)$$ = $$0$$
$$\Rightarrow$$ $$T$$ = $$10$$ or $$60$$ m. T $$\neq$$ 60 m as the width of park is 30 m only.
Therefore, we can say that T = 10 meters. Hence, option A is the correct answer.
Create a FREE account and get:
- All Quant Formulas and shortcuts PDF
- 15 XAT previous papers with solutions PDF
- XAT Trial Classes for FREE
