Ram, Shyam and Hari went out for a 100 km journey. Ram and Hari started the journey in Ram's car at the rate of 25 kmph, while Shyam walked at 5 kmph. After sometime, Hari got off and started walking at the rate of 5kmph and Ram went back to pick up Shyam. All three reached the destination simultaneously. The number of hours required for the trip was:
Solution
Let 'A' be the point from where all started and D is the destination. At 'x' hours both Ram and Hari reached point C, Hari got off and Ram turned back to pick up Shyam. At the same instant, Shyam was at point B.
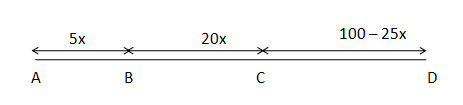
Let 'T' is the total amount of time taken by all three to reach point D.
For Hari,
T = $$x+\dfrac{100-25x}{5}$$ ... (1)
For Ram,
T = $$x+\dfrac{20x*5/6}{25}$$ + $$\dfrac{20x*5/6+100-25x}{25}$$ ... (2)
By equating (1) and (2),
$$x+\dfrac{100-25x}{5}$$ = $$x+\dfrac{20x*5/6}{25}$$ + $$\dfrac{20x*5/6+100-25x}{25}$$
$$\Rightarrow$$ $$x = 3$$ hours.
Therefore, time taken by all to reach destination = $$x+\dfrac{100-25x}{5}$$
$$\Rightarrow$$ 3 + $$\dfrac{100-25*3}{5}$$
$$\Rightarrow$$ 3 + 5
$$\Rightarrow$$ 8 hours
Hence, we can say that option A is the correct answer.
Video Solution

Click on the Email ☝️ to Watch the Video Solution
Create a FREE account and get:
- All Quant Formulas and shortcuts PDF
- 15 XAT previous papers with solutions PDF
- XAT Trial Classes for FREE
