If r is a constant such that $$\mid x^2 - 4x - 13 \mid = r$$ has exactly three distinct real roots, then the value of r is
The quadratic equation of the form $$\mid x^2 - 4x - 13 \mid = r$$ has its minimum value at x = -b/2a, and hence does not vary irrespective of the value of x.
Hence at x = 2 the quadratic equation has its minimum.
Considering the quadratic part : $$\left|x^2-4\cdot x-13\right|$$. as per the given condition, this must-have 3 real roots.
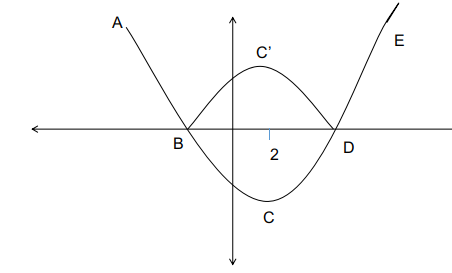
The curve ABCDE represents the function $$\left|x^2-4\cdot x-13\right|$$. Because of the modulus function, the representation of the quadratic equation becomes :
ABC'DE.
There must exist a value, r such that there must exactly be 3 roots for the function. If r = 0 there will only be 2 roots, similarly for other values there will either be 2 or 4 roots unless at the point C'.
The point C' is a reflection of C about the x-axis. r is the y coordinate of the point C' :
The point C which is the value of the function at x = 2, = $$2^2-8-13$$
= -17, the reflection about the x-axis is 17.
Alternatively,
$$\mid x^2 - 4x - 13 \mid = r$$ .
This can represented in two parts :
$$x^2-4x-13\ =\ r\ if\ r\ is\ positive.$$
$$x^2-4x-13\ =\ -r\ if\ r\ is\ negative.$$
Considering the first case : $$x^2-4x-13\ =r$$
The quadraticequation becomes : $$x^2-4x-13-r\ =\ 0$$
The discriminant for this function is : $$b^2-4ac\ =\ 16-\ \left(4\cdot\left(-13-r\right)\right)=68+4r$$
SInce r is positive the discriminant is always greater than 0 this must have two distinct roots.
For the second case :
$$x^2-4x-13+r\ =\ 0$$ the function inside the modulus is negaitve
The discriminant is $$16\ -\ \left(4\cdot\left(r-13\right)\right)\ =\ 68-4r$$
In order to have a total of 3 roots, the discriminant must be equal to zero for this quadratic equation to have a total of 3 roots.
Hence $$\ 68-4r\ =\ 0$$
r = 17, for r = 17 we can have exactly 3 roots.
Video Solution

Your Doubts
Create a FREE account and get:
- All Quant CAT complete Formulas and shortcuts PDF
- 38+ CAT previous year papers with video solutions PDF
- 5000+ Topic-wise Previous year CAT Solved Questions for Free




