In an 8 X 8 chess board a queen placed any where can attack another piece if the piece is present in the same row, or in the same column or in any diagonal position in any possible 4 directions, provided there is no other piece in between in the path from the queen to that piece.
The columns are labelled a to h (left to right) and the rows are numbered 1 to 8 (bottom to top). The position of a piece is given by the combination of column and row labels. For example, position c5 means that the piece is in $$c^{th}$$ column and $$5^{th}$$ row.
If the other pieces are only at positions a1, a3, b4, d7, h7 and h8, then from how many positions the queen cannot attack any of the pieces?
From the diagram we can see that except positions e2, f2, g2 and g5 queen can attack at least one among the given pieces.
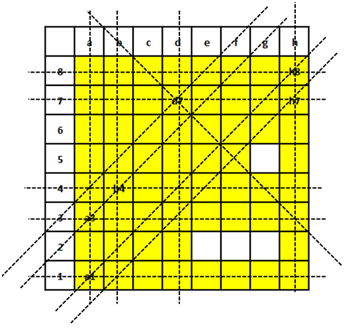
Hence, we can say that there are exactly for position from where queen can’t attack any of the given pieces. Therefore, option C is the correct answer.
Video Solution
Create a FREE account and get:
- All Quant CAT complete Formulas and shortcuts PDF
- 35+ CAT previous papers with video solutions PDF
- 5000+ Topic-wise Previous year CAT Solved Questions for Free
