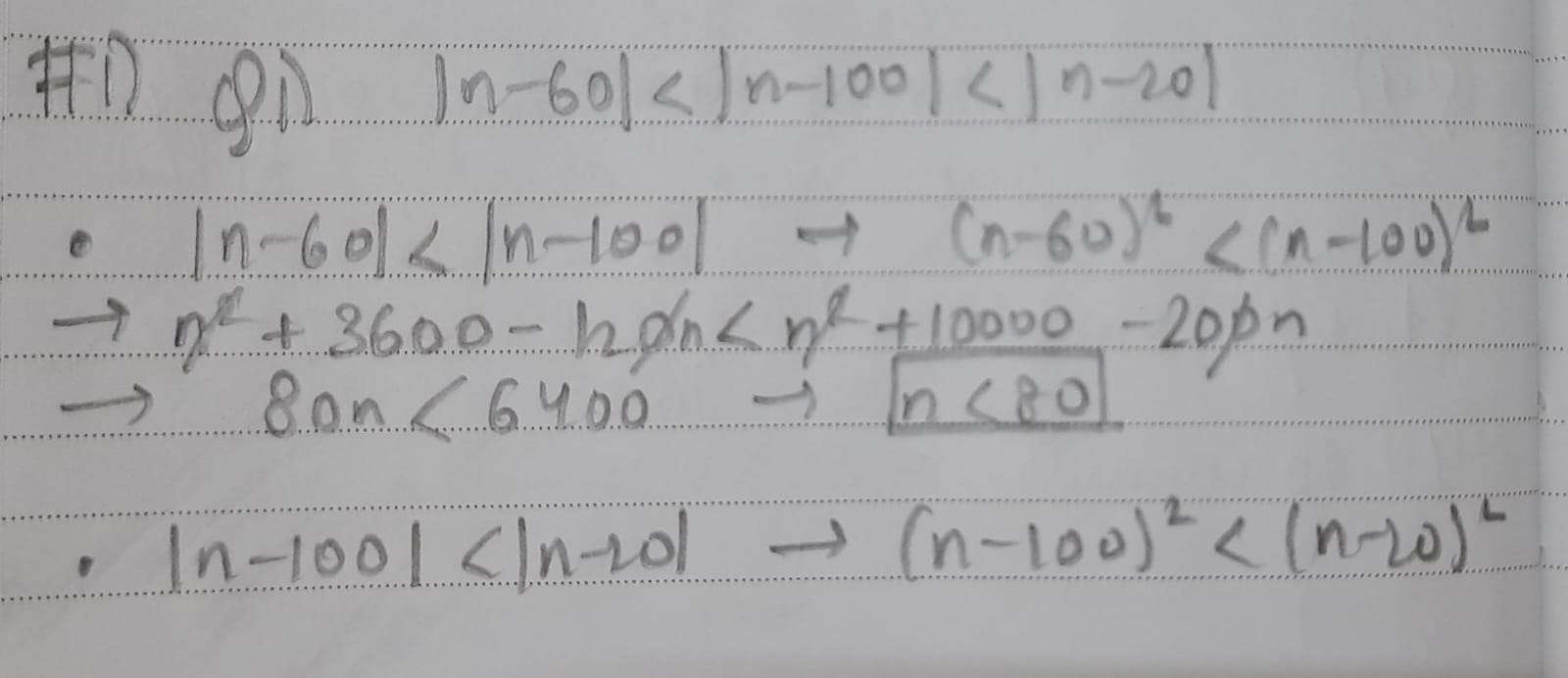The number of integers n that satisfy the inequalities $$\mid n - 60 \mid < \mid n - 100 \mid < \mid n - 20 \mid$$ is
We have $$\mid n - 60 \mid < \mid n - 100 \mid < \mid n - 20 \mid$$.
Now, the difference inside the modulus signified the distance of n from 60, 100, and 20 on the number line. This means that when the absolute difference from a number is larger, n would be further away from that number.
Example: The absolute difference of n and 60 is less than that of the absolute difference between n and 20. Hence, n cannot be $$\le\ 40$$, as then it would be closer to 20 than 60, and closer on the number line would indicate lesser value of absolute difference. Thus we have the condition that n>40.
The absolute difference of n and 100 is less than that of the absolute difference between n and 20. Hence, n cannot be $$\le\ 60$$, as then it would be closer to 20 than 100. Thus we have the condition that n>60.
The absolute difference of n and 60 is less than that of the absolute difference between n and 100. Hence, n cannot be $$\ge80$$, as then it would be closer to 100 than 60. Thus we have the condition that n<80.
The number which satisfies the conditions are 61, 62, 63, 64......79. Thus, a total of 19 numbers.
Alternatively
as per the given condition : $$\mid n - 60 \mid < \mid n - 100 \mid < \mid n - 20 \mid$$.
Dividing the range of n into 4 segments. (n < 20, 20<n<60, 60<n<100, n > 100 )
1) For n < 20.
|n-20| = 20-n, |n-60| = 60- n, |n-100| = 100-n
considering the inequality part :$$\left|n-100\right|<\ \left|n\ -20\right|$$
100 -n < 20 -n,
No value of n satisfies this condition.
2) For 20 < n < 60.
|n-20| = n-20, |n-60| = 60- n, |n-100| = 100-n.
60- n < 100 - n and 100 - n < n - 20
For 100 -n < n - 20.
120 < 2n and n > 60. But for the considered range n is less than 60.
3) For 60 < n < 100
|n-20| = n-20, |n-60| = n-60, |n-100| = 100-n
n-60 < 100-n and 100-n < n-20.
For the first part 2n < 160 and for the second part 120 < 2n.
n takes values from 61 ................79.
A total of 19 values
4) For n > 100
|n-20| = n-20, |n-60| = n-60, |n-100| = n-100
n-60 < n - 100.
No value of n in the given range satisfies the given inequality.
Hence a total of 19 values satisfy the inequality.
Video Solution

Your Doubts
Create a FREE account and get:
- All Quant CAT complete Formulas and shortcuts PDF
- 38+ CAT previous year papers with video solutions PDF
- 5000+ Topic-wise Previous year CAT Solved Questions for Free