Please enter the following details
1000 patients currently suffering from a disease were selected to study the effectiveness of treatment of four types of medicines — A, B, C and D. These patients were first randomly assigned into two groups of equal size, called treatment group and control group. The patients in the control group were not treated with any of these medicines; instead they were given a dummy medicine, called placebo, containing only sugar and starch. The following information is known about the patients in the treatment group.
a. A total of 250 patients were treated with type A medicine and a total of 210 patients were treated with type C medicine.
b. 25 patients were treated with type A medicine only. 20 patients were treated with type C medicine only. 10 patients were treated with type D medicine only.
c. 35 patients were treated with type A and type D medicines only. 20 patients were treated with type A and type B medicines only. 30 patients were treated with type A and type C medicines only. 20 patients were treated with type C and type D medicines only.
d. 100 patients were treated with exactly three types of medicines.
e. 40 patients were treated with medicines of types A, B and C, but not with medicines of type D. 20 patients were treated with medicines of types A, C and D, but not with medicines of type B.
f. 50 patients were given all the four types of medicines. 75 patients were treated with exactly one type of medicine.
The number of patients who were treated with medicine type D was:
Correct Answer: 325
Of the 1000 subjects, only 500 have been considered for the treatment. This constitutes our sample set. Thus the four drugs- A, B, C and D have been administered to this set of 500 individuals, while the rest 500 have been given the placebo. Based on the given information, we can then draw the following 4-set Venn diagram:
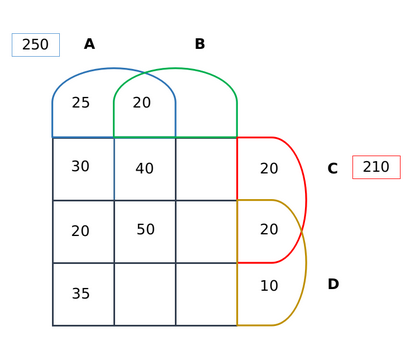
We can solve for the number of patients who were administered the drugs A, B and D excluding C by putting in the values for set A. The required value = 250 - (25+20+30+40+20+50+35) = 30. Based on condition (c), we know that 100 patients were treated with exactly three types of medicines. Thus, we can fill the slot for the number of patients who were administered only B, C and D excluding A by 100 - (40+20+30) = 10.
Similarly, based on condition (f), we know that the candidates who were administered only dug B are 75 - (25+20+10) = 20. Post this, we can easily calculate the number of people administered with only drugs B and C by 210 - (30+20+40+50+10+20+20) = 20. We can fill in the above values to obtain the following diagram:
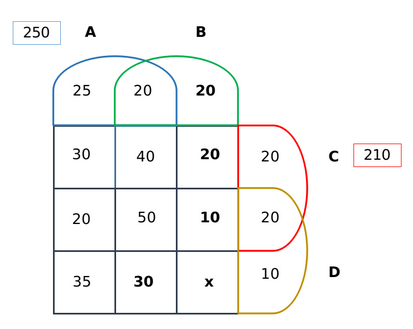
The sum of all the values should add up to 500. On solving for 'x' [which represents the number of people who were administered drugs B and D only], we obtain x = 150. The final representation would appear as follows:
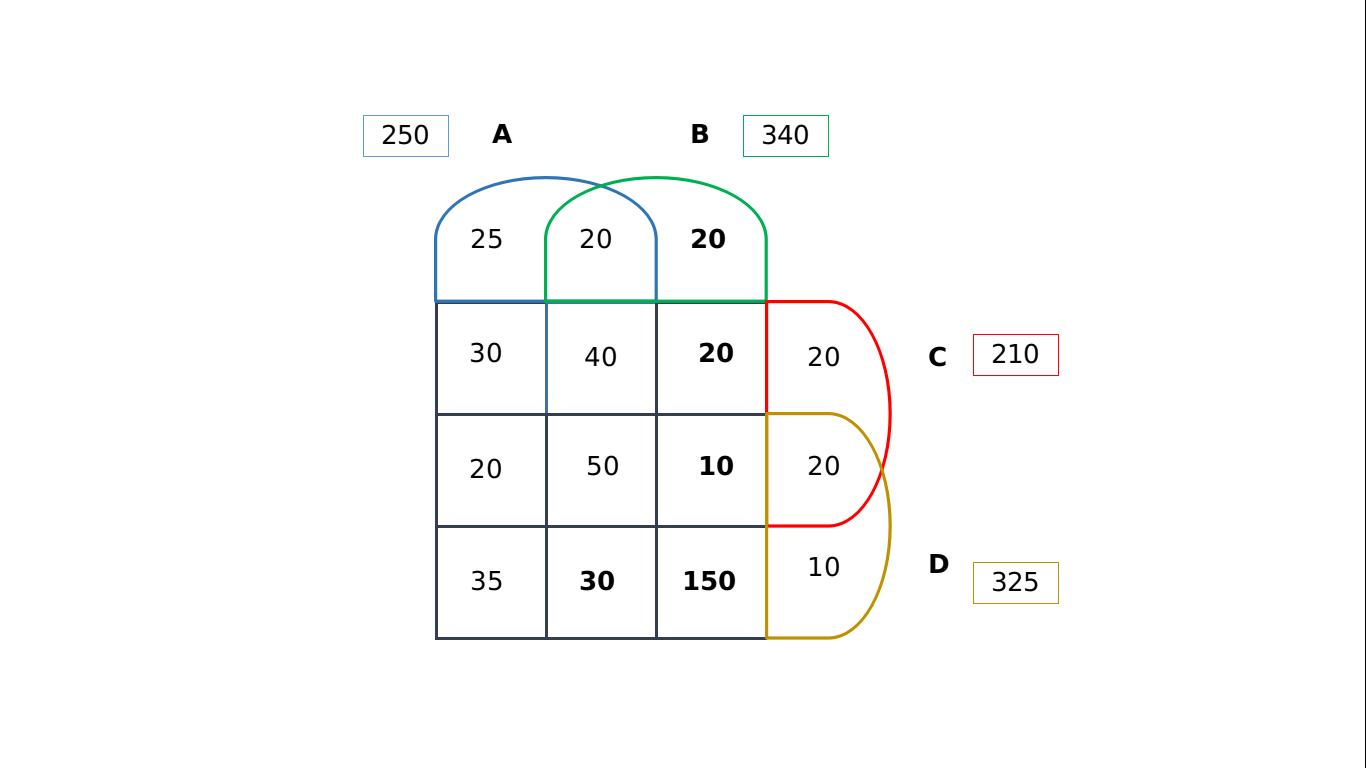
The number of patients who were treated with medicine type D was 325.
Video Solution
Create a FREE account and get:
- All Quant CAT complete Formulas and shortcuts PDF
- 35+ CAT previous year papers with video solutions PDF
- 5000+ Topic-wise Previous year CAT Solved Questions for Free
