Please enter the following details
Six web surfers M, N, O, P, X, and Y each had 30 stars which they distributed among four bloggers A, B, C, and D. The number of stars received by A and B from the six web surfers is shown in the figure below.
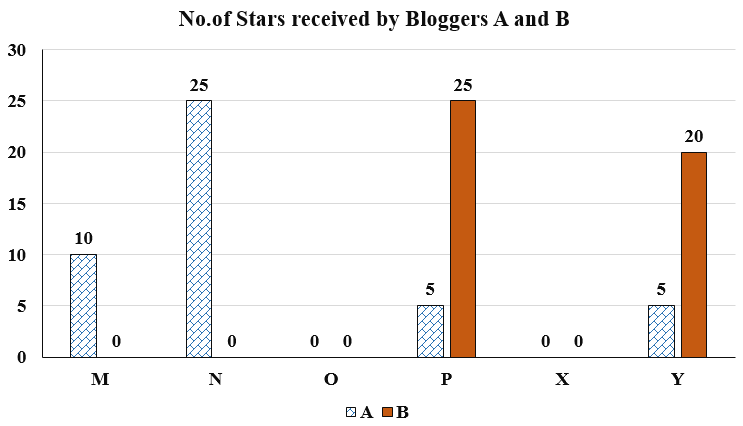
The following additional facts are known regarding the number of stars received by the bloggers from the surfers.
1. The numbers of stars received by the bloggers from the surfers were all multiples of 5 (including 0).
2. The total numbers of stars received by the bloggers were the same.
3. Each blogger received a different number of stars from M.
4. Two surfers gave all their stars to a single blogger.
5. D received more stars than C from Y.
We can note down the data from the chart into the form of a table, that gives us,
We are told that D receives more stars than C from Y. Considering Y has already given 25 stars, it will give 0 stars to C and 5 stars to D.
The only two surfers who have not given any stars to A or B is O and X, and these are the two surfers to give all of their stars to a single blogger.
We are also told that M gives different stars to the four bloggers,
Since he has already given 0 and 10, the remaining distinct stars should add up to 20. The only numbers that are remaining that add up to 20 are 5 and 15.
We know that X rewards one of C or D 30 stars and O rewards one of C or D 30 stars. Given that, M could not have rewarded D 15 stars, since Y rewarded D 5 stars, and D is also going to rewarded 30 stars by O or X, and since the total is same for all, which is 45. This is not possible.
This means that, M rewarded C 15 stars and D 5 stars.
This gives us two cases,
Case-1
Case-2
We can use these two cases to answer the questions,
D was rewarded 45 stars in total.
Create a FREE account and get:
- All Quant CAT complete Formulas and shortcuts PDF
- 38+ CAT previous year papers with video solutions PDF
- 5000+ Topic-wise Previous year CAT Solved Questions for Free
