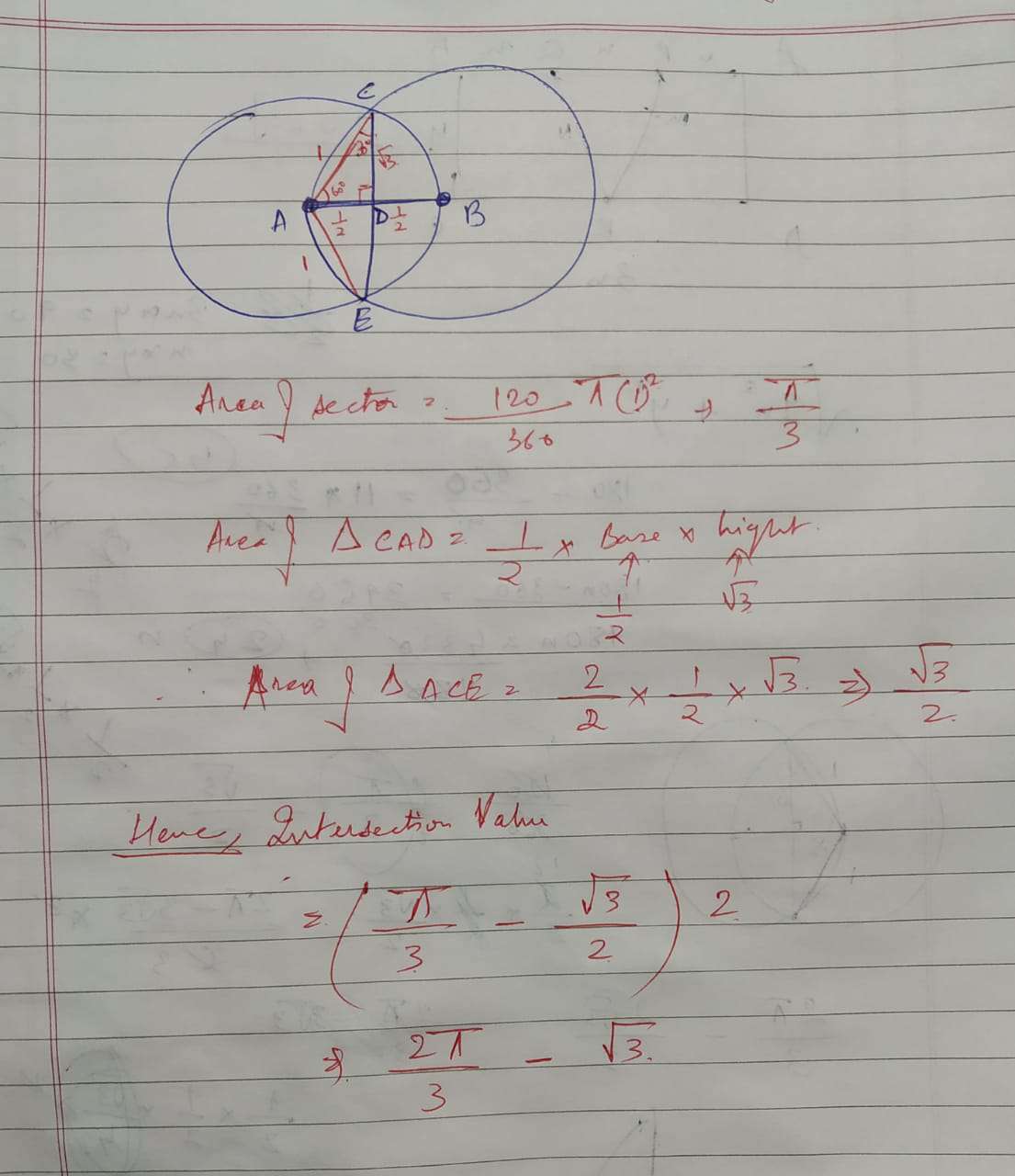Two circles, both of radii 1 cm, intersect such that the circumference of each one passes through the centre of the other. What is the area (in sq. cm.) of the intersecting region?

The circumferences of the two circle pass through each other's centers. Hence, O1A = O1B=O1O2 = 1cm
By symmetry, the line joining the two centres would be bisect AB and would be bisected by AB. As the line joining the center to the midpoint of a chord is perpendicular to the chord, O1O2 and AB are perpendicular bisectors of each other. Suppose they intersect at point P.
O1P = Half of O1O2 = 1/2 cm
So, the angle AO1P = 60 degrees as cos 60 = 1/2
By symmetry, BO1P = 60 degrees.
So, angle AO1B= 120 degrees

In the above, the required area is 2 times A(segment ABO2)(blue region). And A(segment ABO2)(blue region) = A(sector O2AO1B)(blue + red) - A(triangleO1AB )(red)
Area of sector = 120°/360° * $$\pi * 1^2 $$ = $$\pi/3$$
Area of triangle = 1/2 * b * h = 1/2 * (2* 1 cos 30°) * (1/2) = √3/4
Hence, required area = $$\frac{\pi}{3}-\frac{\sqrt 3}{4}$$ . Hence so the required area is 2 times the above value which is $$\frac{2\pi}{3}-\frac{\sqrt 3}{2}$$
Video Solution

Your Doubts
Create a FREE account and get:
- All Quant CAT complete Formulas and shortcuts PDF
- 38+ CAT previous year papers with video solutions PDF
- 5000+ Topic-wise Previous year CAT Solved Questions for Free