XAT 2018 Question Paper
For the following questions answer them individually
XAT 2018 - Question 51
The price of a product is P. A shopkeeper raises its price by X% and then offers a discount of Y% on the raised price. The discounted price again becomes P. If Y is the difference between X and Y, then find X.
XAT 2018 - Question 52
A mixture comprises water and liquids A and B. The volume of water is 1/3rd of the total mixture and the volume of liquids A and B are in the ratio 5:3. To remove the water, the mixture is passed through a porous medium which completely absorbs the water and partially absorbs liquid A. Altogether this porous medium absorbs 200 ml of the initial mixture. If the ratio of volume of liquids A and B in the residual concentrated mixture becomes 7:9 then find the volume of water absorbed by the porous medium.
XAT 2018 - Question 53
A coin of radius 3 cm is randomly dropped on a square floor full of square shaped tiles of side 10 cm each. What is the probability that the coin will land completely within a tile? In other words, the coin should not cross the edge of any tile.
XAT 2018 - Question 54
It takes 2 liters to paint the surface of a solid sphere. If this solid sphere is sliced into 4 identical pieces, how many liters will be required to paint all the surfaces of these 4 pieces.
XAT 2018 - Question 55
Every day a person walks at a constant speed, $$V_1$$ for 30 minutes. On a particular day, after walking for 10 minutes at $$V_1$$, he rested for 5 minutes. He finished the remaining distance of his regular walk at a constant speed, $$V_2$$, in another 30 minutes. On that day, find the ratio of $$V_2$$ and his average speed (i.e., total distance covered /total time taken including resting time).
XAT 2018 - Question 56
A boat, stationed at the North of a lighthouse, is making an angle of 30° with the top of the lighthouse. Simultaneously, another boat, stationed at the East of the same lighthouse, is making an angle of 45° with the top of the lighthouse. What will be the shortest distance between these two boats? The height of the lighthouse is 300 feet. Assume both the boats are of negligible dimensions.
XAT 2018 - Question 57
Two different quadratic equations have a common root. Let the three unique roots of the two equations be A, B and C - all of them are positive integers. If (A + B + C) = 41 and the product of the roots of one of the equations is 35, which of the following options is definitely correct?
XAT 2018 - Question 58
An antique store has a collection of eight clocks. At a particular moment, the displayed times on seven of the eight clocks were as follows: 1:55 pm, 2:03 pm, 2:11 pm, 2:24 pm, 2:45 pm, 3:19 pm and 4:14 pm. If the displayed times of all eight clocks form a mathematical series, then what was the displayed time on the remaining clock?
XAT 2018 - Question 59
The number of boys in a school was 30 more than the number of girls. Subsequently, a few more girls joined the same school. Consequently, the ratio of boys and girls became 3:5. Find the minimum number of girls, who joined subsequently.
Assume that there was at least one girl at the start.
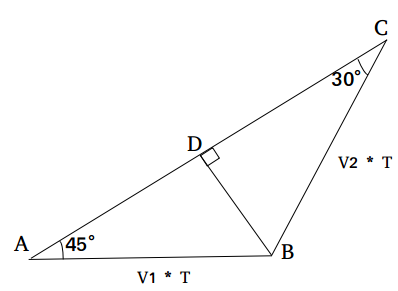
XAT 2018 - Question 60
A girl travels along a straight line, from point A to B at a constant speed, $$V_1$$ meters/sec for T seconds. Next, she travels from point B to C along a straight line, at a constant speed of $$V_2$$ meters/sec for another T seconds. BC makes an angle 105° with AB. If CA makes an angle 30° with BC, how much time will she take to travel back from point C to A at a constant speed of $$V_2$$ meters/sec, if she travels along a straight line from C to A?
Two Factor Authentication
Incase of any issue contact support@cracku.in



.webp)