XAT 2014 Question Paper
For the following questions answer them individually
XAT 2014 - Question 61
Consider the formula, $$S=\frac{\alpha\times\omega}{\tau+\rho\times\omega}$$ positive integers. If ⍵ is increased and ⍺, τ and ρ are kept constant, then S:
XAT 2014 - Question 62
Prof. Suman takes a number of quizzes for a course. All the quizzes are out of 100. A student can get an A grade in the course if the average of her scores is more than or equal to 90.Grade B is awarded to a student if the average of her scores is between 87 and 89 (both included). If the average is below 87, the student gets a C grade. Ramesh is preparing for the last quiz and he realizes that he will score a minimum of 97 to get an A grade. After the quiz, he realizes that he will score 70, and he will just manage a B. How many quizzes did Prof. Suman take?
XAT 2014 - Question 63
A polynomial y=$$ax^{3} + bx^{2 }+ cx + d$$ intersects x-axis at 1 and -1, and y-axis at 2. The value of b is:
XAT 2014 - Question 64
The probability that a randomly chosen positive divisor of $$10^{29}$$ is an integer multiple of $$10^{23}$$ is: $$a^{2} /b^{2} $$, then ‘b - a’ would be:
XAT 2014 - Question 65
Circle $$C_{1}$$ has a radius of 3 units. The line segment PQ is the only diameter of the circle which is parallel to the X axis. P and Q are points on curves given by the equations $$y = a^{x} and y = 2a^{x}$$ respectively, where a < 1. The value of a is:
XAT 2014 - Question 66
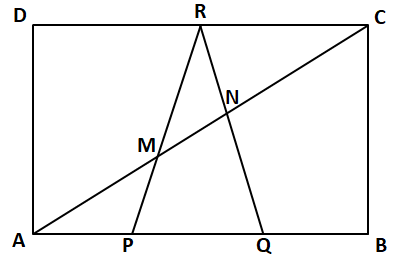
Consider a rectangle ABCD of area 90 units. The points P and Q trisect AB, and R bisects CD. The
diagonal AC intersects the line segments PR and QR at M and N respectively. What is the area of the quadrilateral PQNM?
XAT 2014 - Question 67
Two numbers, $$297_{B}$$ and $$792_{B}$$ , belong to base B number system. If the first number is a factor of the second number then the value of B is:
XAT 2014 - Question 68
A teacher noticed a strange distribution of marks in the exam. There were only three distinct
scores: 6, 8 and 20. The mode of the distribution was 8. The sum of the scores of all the students was 504. The number of students in the in most populated category was equal to the sum of the number of students with lowest score and twice the number of students with the highest score. The total number of students in the class was:
XAT 2014 - Question 69
Read the following instruction carefully and answer the question that follows:
Expression $$\sum_{n=1}^{13}\frac{1}{n}$$ can also be written as $$\frac{x}{13!}$$ What would be the remainder if x is divided by 11?
XAT 2014 - Question 70
A rectangular swimming pool is 48 m long and 20 m wide. The shallow edge of the pool is 1 m deep.
For every 2.6 m that one walks up the inclined base of the swimming pool, one gains an elevation of 1 m. What is the volume of water (in cubic meters), in the swimming pool? Assume that the pool is filled up to the brim.v
Two Factor Authentication
Incase of any issue contact support@cracku.in


.webp)


