Consider a rectangle ABCD of area 90 units. The points P and Q trisect AB, and R bisects CD. The
diagonal AC intersects the line segments PR and QR at M and N respectively. What is the area of the quadrilateral PQNM?

Let us draw the figure according to the available information, 

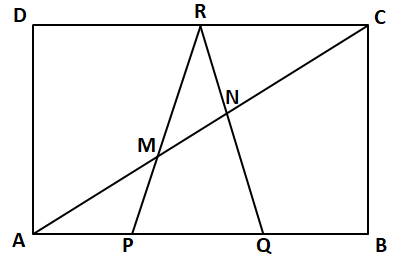
In $$\triangle$$ AMP and $$\triangle$$ CMR

$$\angle$$ MAP = $$\angle$$ MCR

$$\angle$$ AMP = $$\angle$$ CMR

Therefore, we can say that $$\triangle$$ AMP $$\sim$$ $$\triangle$$ CMR

Hence, we can say that $$\dfrac{AP}{CR}=\dfrac{MP}{MR}$$

$$\Rightarrow$$ $$\dfrac{AB/3}{AB/2}=\dfrac{MP}{MR}$$

$$\Rightarrow$$ $$MR=\dfrac{3}{2}*MP$$

Therefore, we can say that $$\Rightarrow$$ $$MR=\dfrac{3}{5}*RP$$   ... (1)

Similarly, in $$\triangle$$ ANQ and $$\triangle$$ CNR

$$\angle$$ NAQ = $$\angle$$ NCR

$$\angle$$ ANQ = $$\angle$$ CNR

Therefore, we can say that $$\triangle$$ ANQ $$\sim$$ $$\triangle$$ CNR

Hence, we can say that $$\dfrac{AQ}{CR}=\dfrac{NQ}{NR}$$

$$\Rightarrow$$ $$\dfrac{2AB/3}{AB/2}=\dfrac{NQ}{NR}$$

$$\Rightarrow$$ $$NR=\dfrac{3}{4}*NQ$$

Therefore, we can say that $$\Rightarrow$$ $$NR=\dfrac{3}{7}*RQ$$  ... (2)

In $$\triangle$$ RMN and $$\triangle$$ RPQ 

$$\dfrac{\text{Area of triangle RMN}}{\text{Area of triangle RPQ}} = \dfrac{0.5*RM*RN*sinMRN}{0.5*RP*RQ*sinPRQ}$$

$$\text{Area of triangle RMN}=\dfrac{3}{5}*\dfrac{3}{7}*\text{Area of triangle RPQ}$$

We know that, Area of triangle RPQ = 1/6*Area of rectangle ABCD = 1/6*90 = 15 sq. units

$$\Rightarrow$$ $$\text{Area of triangle RMN}=\dfrac{3}{5}*\dfrac{3}{7}*15$$ = $$\dfrac{27}{7}$$ sq. units

Hence, the area of the quadrilateral PQNM = 15 - $$\dfrac{27}{7}$$ = $$\dfrac{78}{7}=11\dfrac{1}{7}$$ sq. units. Therefore, option D is the correct answer.