PGDBA 2019 Question Paper
Answer the questions based on the following information.
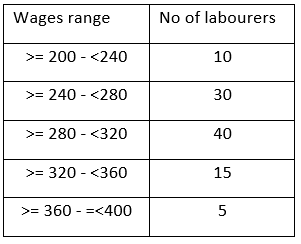
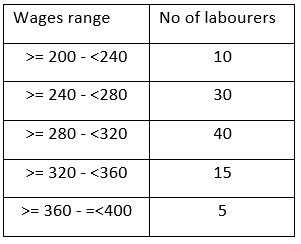
The following bar diagram represents the number of daily wages (in rupees) of 100 labourers in different wage classes on a construction site. Here the class interval a-b includes all wages (in rupees) greater than or equal to a and less than b except for the interval 360-400, where both the end points are included.
No.of labourers

Wages in Rupees
PGDBA 2019 - Question 3
The maximum wage (in Rupees), such that at least 50% of the labourers definitely earn more than that, is
Answer the questions based on the following information.
The following table gives month-wise arrivals of foreign tourists in India in the years 2016 & 2017.
Table: Month-wise Arrivals of Foreign Tourists (in Thousands) in India (2016-2017)

PGDBA 2019 - Question 4
In which month of 2017 is the percentage increase over the corresponding month of the previous year the minimum?
PGDBA 2019 - Question 5
In which month of 2017 is the percentage increase over the previous month the maximum?
For the following questions answer them individually
PGDBA 2019 - Question 6
If $$ f(x) = \log_{e}({\frac{2 - x}{9 - x^2}})$$, then the domain of the function $$f$$ is
PGDBA 2019 - Question 7
If the system of linear equations
$$2x+ y+7z = a$$
$$6x-2y+11z = b$$
$$2x-y+3z = c$$
has infinite number of solutions, then $$a, b, c$$ must satisfy
PGDBA 2019 - Question 8
If $$\alpha, \beta$$ are the roots of the equation $$x^2 + 3x - 3$$ , then the value of $$(\alpha + 1)^{-1} + (\beta +1)^{-1}$$ is equal to
PGDBA 2019 - Question 9
The number of real roots of the equation
$$(e^x + e^{-x})^3 + 3(e^x + e^{-x})^2 + 3(e^x + e^{-x}) = 7$$
PGDBA 2019 - Question 10
Let $$x = -\frac{1}{1!}\cdot\frac{3}{4} + \frac{1}{2!}\cdot(\frac{3}{4})^2 -\frac{1}{3!}\cdot(\frac{3}{4})^3 +$$.... and $$y = x - \frac{x^2}{2} + \frac{x^3}{3} - $$..... then the value of y is
Two Factor Authentication
Incase of any issue contact support@cracku.in