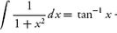PGDBA 2019 Question Paper
For the following questions answer them individually
PGDBA 2019 - Question 21
Let the function $$f$$ be defined on the set of real numbers by
$$ f(x) = \begin{cases}x^2 - x, & if x < 1\\\frac{x^2 - 1}{3}, &if x \geq 1\end{cases}$$ then which of the following statement is TRUE ?
PGDBA 2019 - Question 22
If $$f'(x)$$ and $$g'(x)$$ exist for all $$x \in R$$, and if $$f'(x)>g'(x)$$ for all $$x \in R$$, then the curve $$y = f(x)$$ and $$y = g(x)$$ in the $$xy$$-plane
PGDBA 2019 - Question 23
The value of the integral $$\int_{-\frac{1}{\sqrt{3}}}^{\frac{1}{\sqrt{3}}} (\frac{x^2 - \tan x}{1 + x^2})dx$$ is equal to
PGDBA 2019 - Question 24
The area enclosed between the parabolas $$y^2 = 16(1 + x )$$ and $$y^2 = 16(1 - x)$$ is
PGDBA 2019 - Question 25
Let $$[x]$$ denote the greatest integer less than or equal to $$x$$. The value of the integral $$\int_{0}^{\sqrt{2}} [x^2]e^x dx$$ is equal to
PGDBA 2019 - Question 26
A function $$f(x) = ax^2 + bx + c$$, where $$a, b, c \in R$$, satisfies the property $$f(x) < x$$ for all $$x \in R$$. Then which of the following statements must always be TRUE?
PGDBA 2019 - Question 27
The foot of the ladder RS in the following figure is slipping away from the wall RO.

Then the point P(a fixed point on the ladder) lies on
PGDBA 2019 - Question 28
Given that
$$\lim_{x\rightarrow0}\frac{ae^x - be^{-x}}{x + \sin x} = 1$$
Then the value of ab is
PGDBA 2019 - Question 29
If $$\mid \frac{x + 1}{x - 1} \mid > \frac{x + 1}{x - 1}$$, then
PGDBA 2019 - Question 30
How many $$6 \times 7$$ matrices are there with entries in {0,1} such that all the row totals and column totals are odd numbers?
Two Factor Authentication
Incase of any issue contact support@cracku.in