IPMAT Indore 2024 Question Paper
For the following questions answer them individually
IPMAT Indore 2024 - Question 1
If $$4^{\log_2 x} - 4x + 9^{\log_3 y} - 16y + 68 = 0$$, then $$y - x$$ equals:
789
456
123
0.-
Clear All
IPMAT Indore 2024 - Question 2
A fruit seller has oranges, apples, and bananas in the ratio 3 : 6 : 7. If the number of oranges is a multiple of both 5 and 6, then the minimum number of fruits the seller has is:
789
456
123
0.-
Clear All
IPMAT Indore 2024 - Question 3
The number of real solutions of the equation $$(x^2 -15x + 55)^{x^2 - 5x + 6} = 1$$ is:
789
456
123
0.-
Clear All
IPMAT Indore 2024 - Question 4
The following table shows the number of employees and their median age in eight companies located in a district.
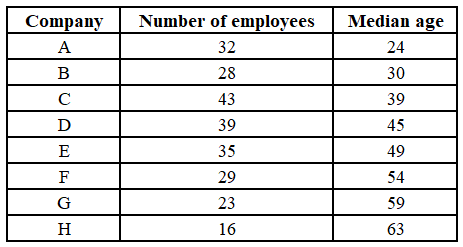
It is known that the age of all employees are integers. It is known that the age of every employee in A is strictly less than the age of every employee in B, the age of every employee in B is strictly less than the age of every employee in C, ..., the age of every employee in G is strictly less than the age of every employee in H. The highest possible age of an employee of company A is:
789
456
123
0.-
Clear All
IPMAT Indore 2024 - Question 5
Person A borrows Rs. 4000 from another person B for a duration of 4 years. He borrows a portion of it at 3% simple interest per annum, while the rest at 4% simple interest per annum. If B gets Rs. 520 as total interest, then the amount A borrowed at 3% per annum in Rs. is:
789
456
123
0.-
Clear All
IPMAT Indore 2024 - Question 6
The number of triangles with integer sides and with perimeter 15 is:
789
456
123
0.-
Clear All
IPMAT Indore 2024 - Question 7
If $$A = \begin{bmatrix}x_1 & x_2 & 7 \\y_1 & y_2 & y_3 \\z_1 & 8 & 3 \end{bmatrix}$$ is a matrix such that the sum of all three elements along any row, column or diagonal are equal to each other, then the value of determinant of A is:
789
456
123
0.-
Clear All
IPMAT Indore 2024 - Question 8
The number of factors of 1800 that are multiple of 6 is:
789
456
123
0.-
Clear All
IPMAT Indore 2024 - Question 9
The following table shows the number of employees and their median age in eight companies located in a district.
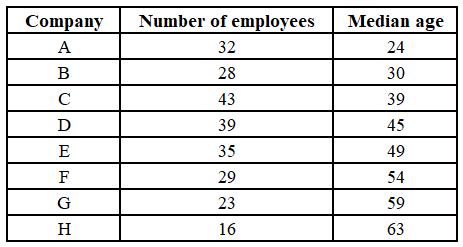
It is known that the age of all employees are integers. It is known that the age of every employee in A is strictly less than the age of every employee in B, the age of every employee in B is strictly less than the age of every employee in C, ..., the age of every employee in G is strictly less than the age of every employee in H.
The median age of employees across the eight companies is:
789
456
123
0.-
Clear All
IPMAT Indore 2024 - Question 10
Let $$\triangle ABC$$ be a triangle right-angled at B with AB = BC = 18. The area of the largest rectangle that can be inscribed in this triangle and has B as one of the vertices is:
789
456
123
0.-
Clear All
