The following table shows the number of employees and their median age in eight companies located in a district.

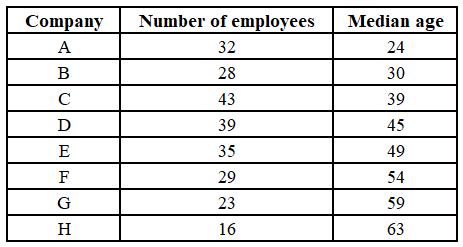
It is known that the age of all employees are integers. It is known that the age of every employee in A is strictly less than the age of every employee in B, the age of every employee in B is strictly less than the age of every employee in C, ..., the age of every employee in G is strictly less than the age of every employee in H.

The median age of employees across the eight companies is: